Giải mục II trang 64, 65 SGK Toán 7 tập 2 - Cánh diềuỞ Hình 6, diện tích các hình chữ nhật (I), (II) lần lượt là Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên...
Lựa chọn câu để xem lời giải nhanh hơn
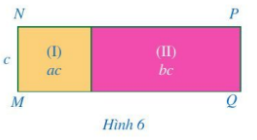
HĐ 2 Ở Hình 6, diện tích các hình chữ nhật (I), (II) lần lượt là A=ac,B=bc. Biết MN=c.
a) Tính NP. b) So sánh: (A+B):c và A:c+B:c. Phương pháp giải: a) NP là độ dài của một cạnh hình chữ nhật. Để tính được NP ta phải tính được diện tích của hình chứa NP. Hoặc tính độ dài của hai cạnh hợp thành NP với diện tích của hình (I), (II) đã cho. b) Thực hiện hai phép chia (A+B):c và A:c+B:crồi so sánh kết quả. Lời giải chi tiết: a) Ta có: Diện tích hình chữ nhật MNPQ bằng diện tích hình chữ nhật (I) + diện tích hình chữ nhật (II) =ac+bc=(a+b).c. Mà MN = c Do đó NP = (a+b).c:c=a+b. b) Ta có: (A+B):c=(ac+bc):c=a+bA:c+B:c=ac:c+bc:c=a+b Vậy (A+B):c =A:c+B:c. HĐ 3 Cho đa thức P(x)=4x2+3x và đơn thức Q(x)=2x. a) Hãy chia từng đơn thức (của biến x) có trong đa thức P(x) cho đơn thức Q(x). b) Hãy cộng các thương vừa tìm được. Phương pháp giải: a) Để chia từng đơn thức có trong đa thức P(x) cho đơn thức Q(x), trước hết ta phải xác định được các đơn thức có trong đa thức P(x) rồi thực hiện phép tính. b) Cộng các thương vừa tìm được ở phần a) với nhau. Lời giải chi tiết: a) Các đơn thức có trong đa thức P(x) là: 4x2;3x. Chia từng đơn thức (của biến x) có trong đa thức P(x) cho đơn thức Q(x) được kết quả lần lượt là: 4x2:2x=(4:2).(x2:x)=2x. 3x:2x=(3:2).(x:x)=32. b) Cộng các thương vừa tìm được =2x+32. LT - VD 2 Tính: (12x4−14x3+x):(−18x). Phương pháp giải: Muốn chia đa thức P cho đơn thức Q (Q ≠ 0) khi số mũ của biến ở mỗi đơn thức của P lớn hơn hoặc bằng số mũ của biến đó trong Q, ta chia mỗi đơn thức của P cho đơn thức Q rồi cộng các thương với nhau. Lời giải chi tiết: (12x4−14x3+x):(−18x)=12x4:(−18x)−14x3:(−18x)+x:(−18x)=(12:−18).(x4:x)−(14:−18).(x3:x)+(1:−18).(x:x)=−4.x4−1−(−2).x3−1+(−8).x1−1=−4x3+2x2−8
|