Giải mục I trang 44, 45 SGK Toán 10 tập 1 - Cánh diềua) Quan sát Hình 17 và cho biết dấu của tam thức bậc hai f(x) = x^2 - 2x + 2 b) Quan sát Hình 20 và cho biết dấu của tam thức bậc hai f(x) = - x^2 + 4x - 4 Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Lựa chọn câu để xem lời giải nhanh hơn
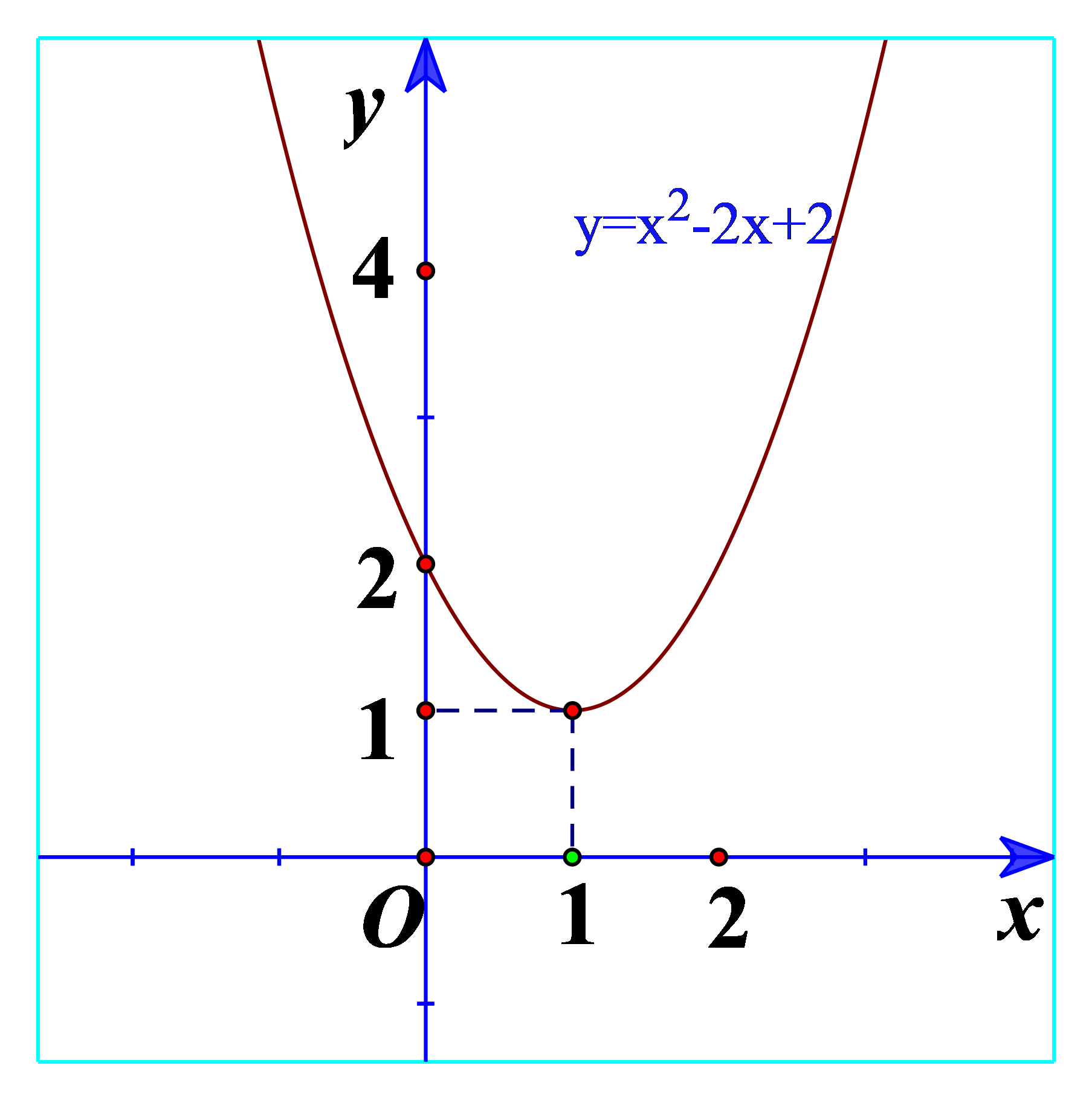
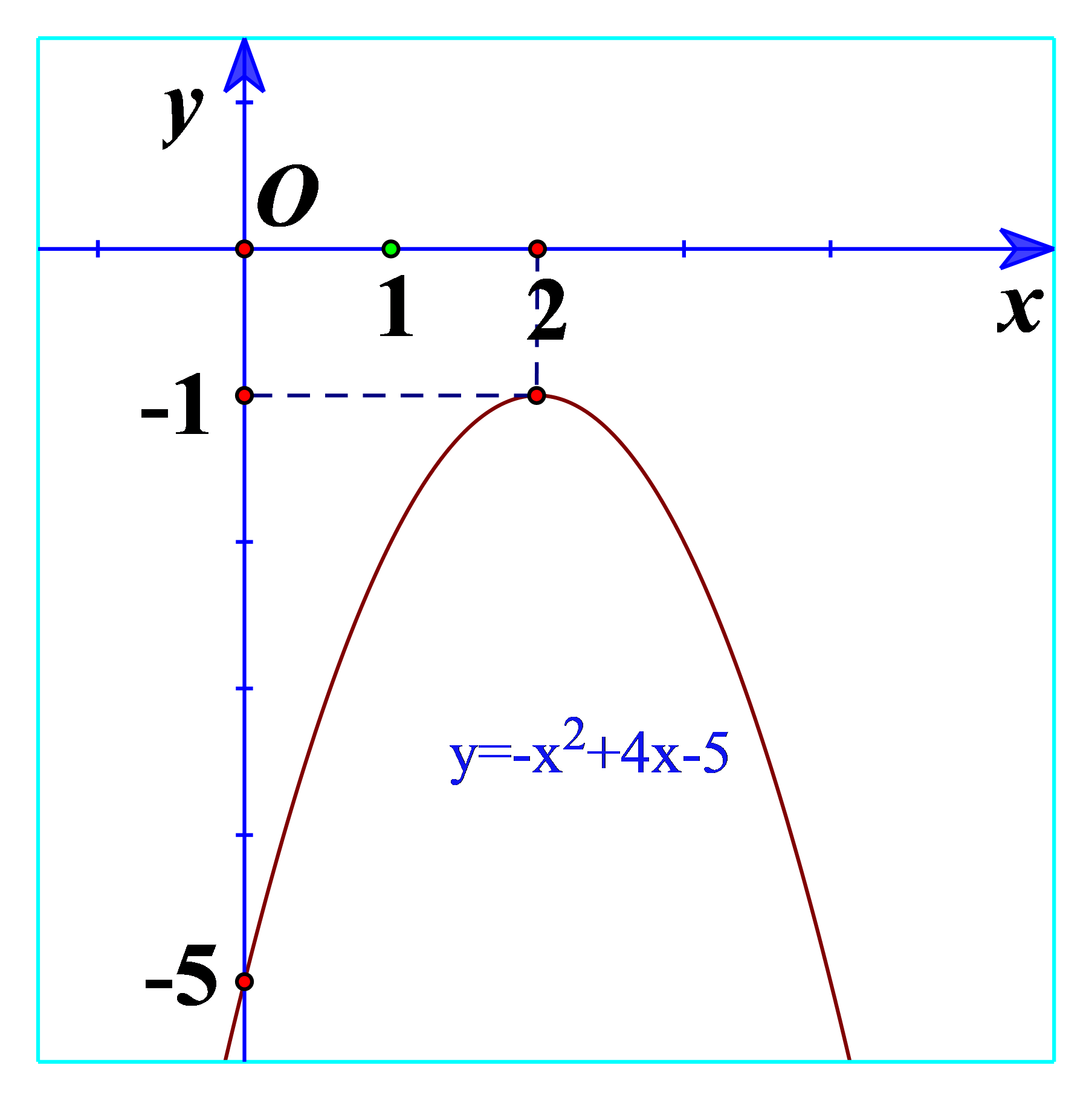
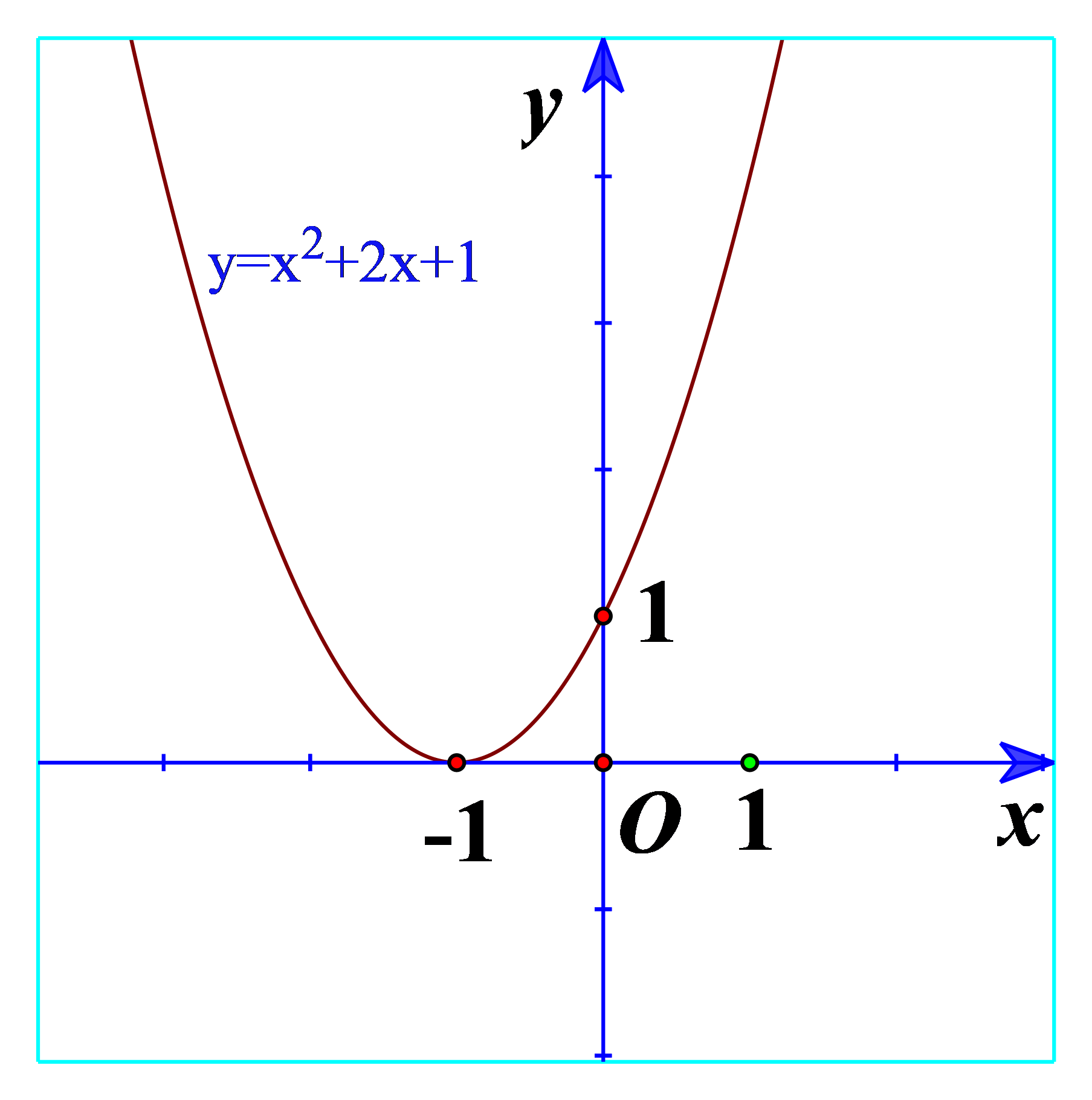
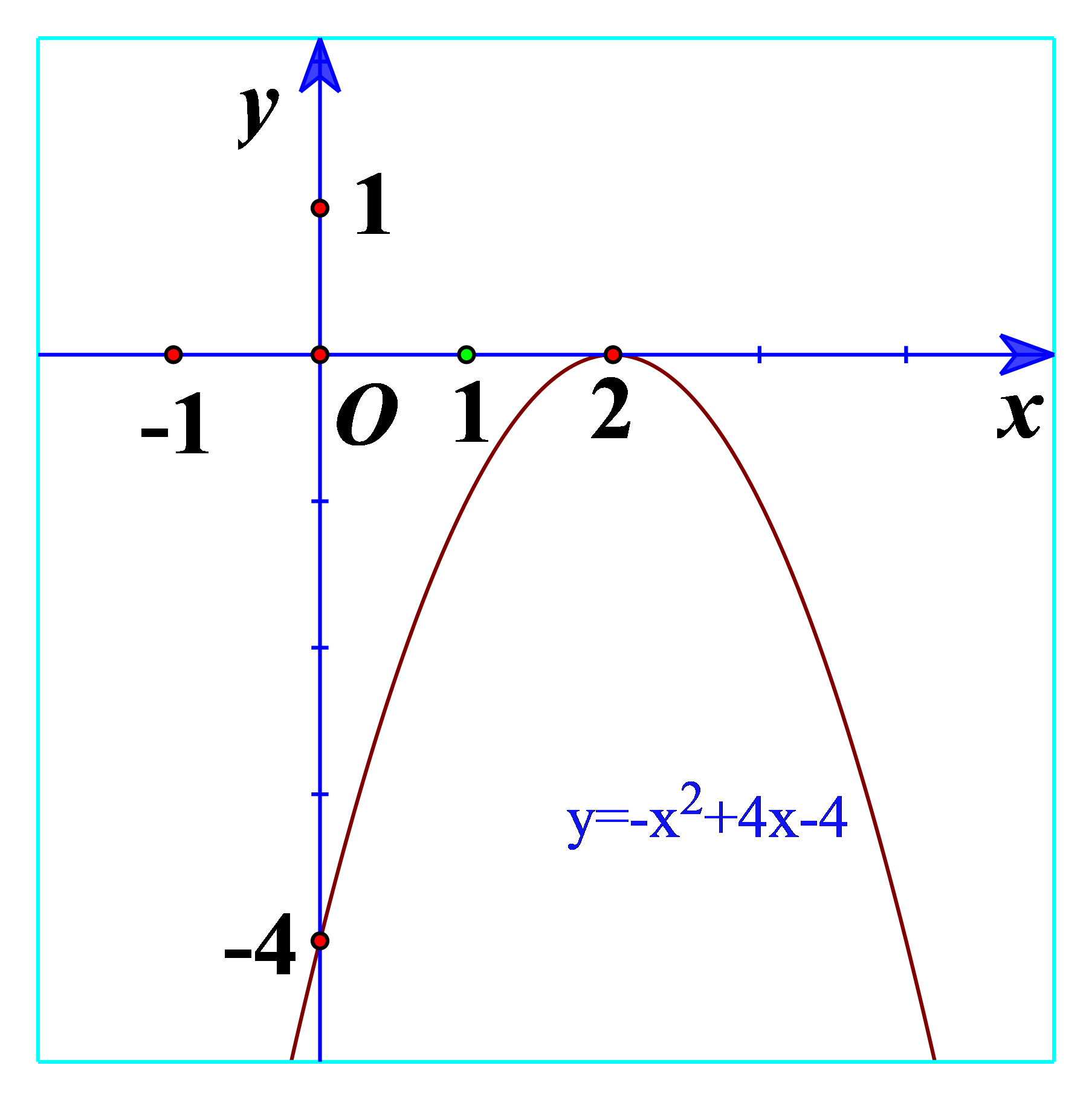
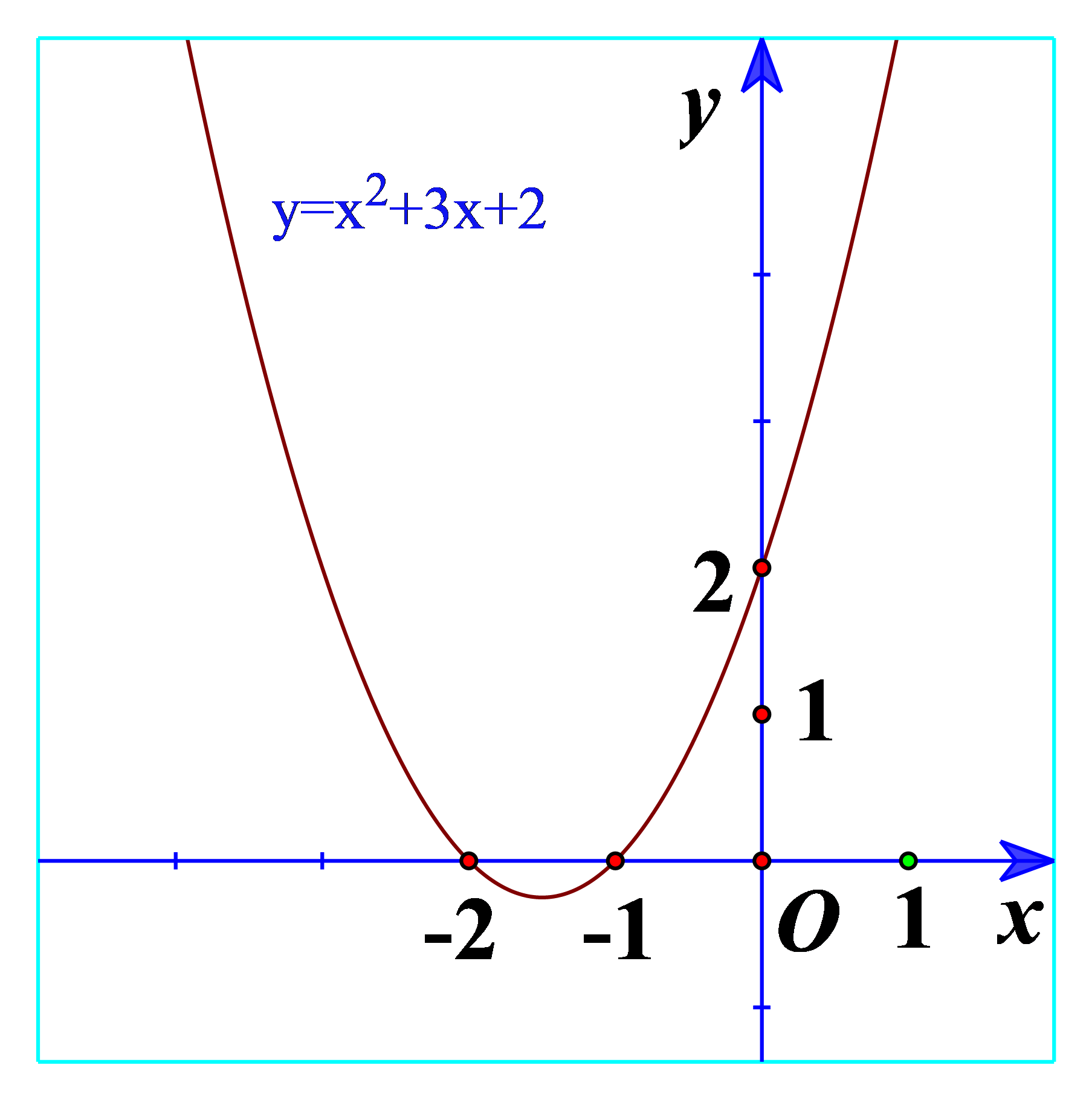
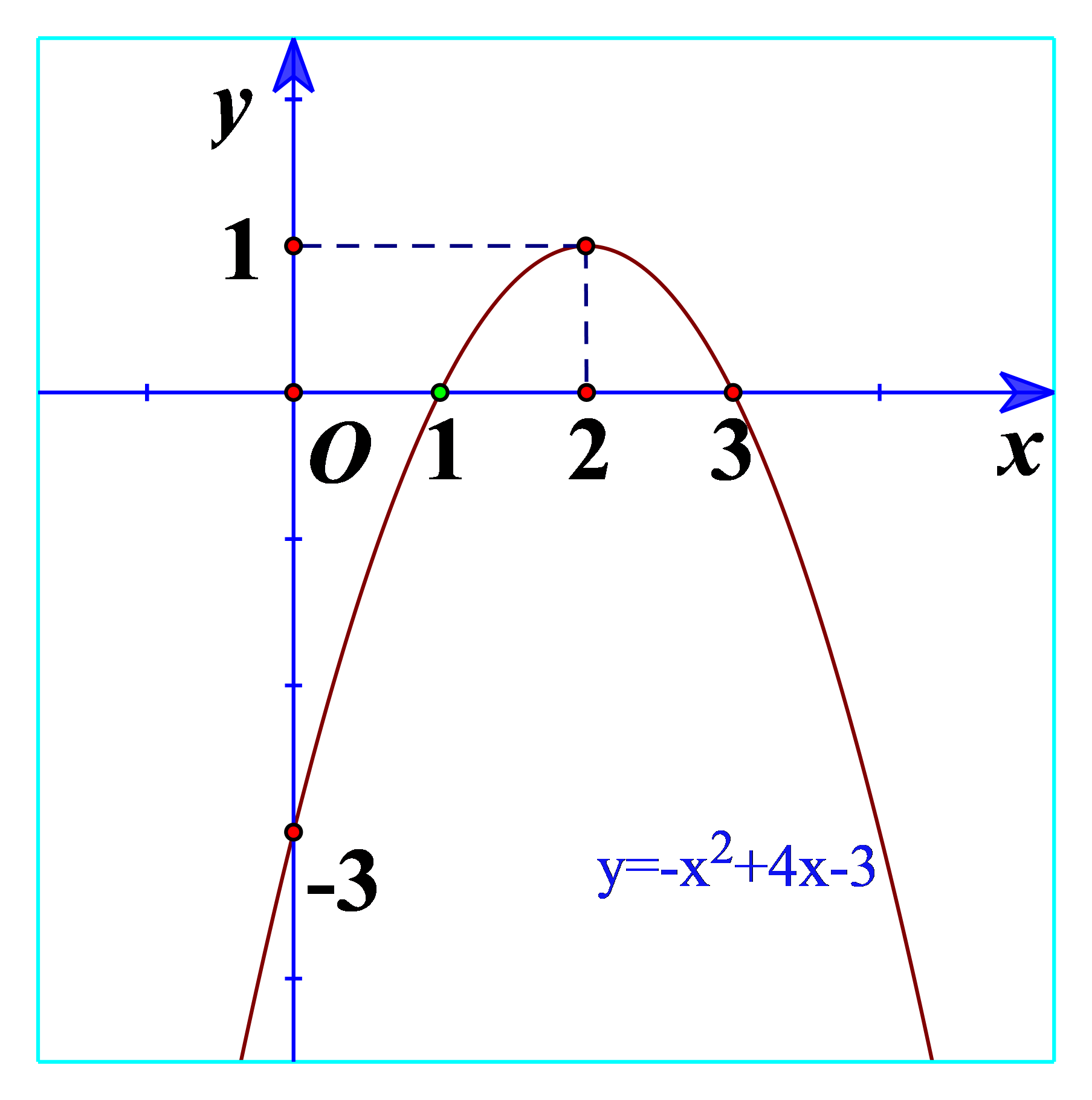
Hoạt động 1 a) Quan sát Hình 17 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} - 2x + 2\) b) Quan sát Hình 18 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 5\) c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số a trong trường hợp \(\Delta < 0\). Phương pháp giải: a) \(a{x^2} + bx + c > 0\) ứng với phần parabol \(y = a{x^2} + bx + c\) nằm phía trên trục hoành. b) \(a{x^2} + bx + c < 0\) ứng với phần parabol \(y = a{x^2} + bx + c\) nằm phía dưới trục hoành. c) Rút ra nhận xét. Lời giải chi tiết: a) Ta thấy đồ thị nằm trên trục hoành nên \(f\left( x \right) = {x^2} - 2x + 2 > 0\). b) Ta thấy đồ thị nằm dưới trục hoành nên \(f\left( x \right) = - {x^2} + 4x - 5 < 0\). c) Ta thấy \(f\left( x \right) = {x^2} - 2x + 2\) có hệ số a=1>0 và \(f\left( x \right) = {x^2} - 2x + 2 > 0\) \(f\left( x \right) = - {x^2} + 4x - 5\) có hệ số a=-1 Như thế, khi \(\Delta < 0\) thì tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) cùng dấu với hệ số a. Hoạt động 2 a) Quan sát Hình 19 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} + 2x + 1\) b) Quan sát Hình 20 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 4\) c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số a trong trường hợp \(\Delta = 0\). Phương pháp giải: a) Xét giao điểm của đồ thị và trục hoành. Xét dấu của tam thức bậc hai \(f\left( x \right) = {x^2} + 2x + 1\). b) Xét giao điểm của đồ thị và trục hoành. Xét dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 4\). c) Rút ra nhận xét. Lời giải chi tiết: a) Từ đồ thị ta thấy \({x^2} + 2x + 1 \ge 0\forall x\) Và \({x^2} + 2x + 1 > 0\forall x \in \mathbb{R}\backslash \left\{ { - 1} \right\}\) b) Từ đồ thị ta thấy \( - {x^2} + 4x - 4 \le 0\forall x\) Và \( - {x^2} + 4x - 4 < 0\forall x \in \mathbb{R}\backslash \left\{ { - 2} \right\}\) c) Nếu \(\Delta = 0\) thì \(f\left( x \right)\) cùng dấu với dấu của hệ số a, với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ - b}}{{2a}}} \right\}\) Hoạt động 3 a) Quan sát Hình 21 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} + 3x + 2\) tùy theo các khoảng của x. b) Quan sát Hình 22 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 3\) tùy theo các khoảng của x. c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số tùy theo các khoảng của x trong trường hợp \(\Delta > 0\). Phương pháp giải: a) Xét các khoảng \(\left( { - \infty ; - 2} \right);\left( { - 2; - 1} \right);\left( { - 1; + \infty } \right)\) b) Xét các khoảng \(\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)\) c) Rút ra nhận xét. Lời giải chi tiết: a) Ta thấy trên \(\left( { - \infty ; - 2} \right)\): Đồ thị nằm trên trục hoành => \(f\left( x \right) = {x^2} + 3x + 2 > 0\)\(\forall x \in \left( { - \infty ; - 2} \right)\) Trên \(\left( { - 2; - 1} \right)\): Đồ thị nằm dưới trục hoành => \(f\left( x \right) = {x^2} + 3x + 2 < 0\)\(\forall x \in \left( { - 2; - 1} \right)\) Trên \(\left( { - 1; + \infty } \right)\): Đồ thị nằm trên trục hoành => \(f\left( x \right) = {x^2} + 3x + 2 > 0\)\(\forall x \in \left( { - 1; + \infty } \right)\) b) Trên \(\left( { - \infty ;1} \right)\): Đồ thị nằm dưới trục hoành => \(f\left( x \right) = - {x^2} + 4x - 3 < 0\)\(\forall x \in \left( { - \infty ;1} \right)\) Trên \(\left( {1;3} \right)\): Đồ thị nằm trên trục hoành => \(f\left( x \right) = - {x^2} + 4x - 3 > 0\)\(\forall x \in \left( {1;3} \right)\) Trên \(\left( {3; + \infty } \right)\): Đồ thị nằm dưới trục hoành => \(f\left( x \right) = - {x^2} + 4x - 3 < 0\)\(\forall x \in \left( {3; + \infty } \right)\) c) Nếu \(\Delta > 0\) thì \(f\left( x \right)\) cùng dấu vưới hệ số a với mọi x thuộc các khoảng \(\left( { - \infty ;{x_1}} \right)\) và \(\left( {{x_2}; + \infty } \right)\); \(f\left( x \right)\) trái dấu với hệ số a với mọi x thuộc khoảng \(\left( {{x_1};{x_2}} \right)\), trong đó \({x_1},{x_2}\) là hai nghiệm của \(f\left( x \right)\) và \({x_1} < {x_2}\).
|