Giải mục 3 trang 88, 89 SGK Toán 8 tập 2 - Kết nối tri thứcBạn Tròn đang đứng ở vị trí điểm A Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên
Lựa chọn câu để xem lời giải nhanh hơn
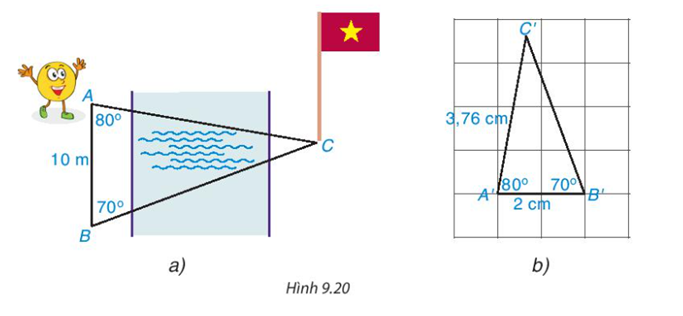
HĐ3 Video hướng dẫn giải Bạn Tròn đang đứng ở vị trí điểm A bên bờ sông và nhờ anh Pi tính giúp khoảng cách từ chỗ mình đứng đến chân một cột cờ tại điểm C bên kia sông (H.9.20a). Anh Pi lấy một vị trí B sao cho AB=10m, \(\widehat {ABC} = {70^o}{,^{}}\widehat {BAC} = {80^o}\) và vẽ một tam giác A'B'C' trên giấy với A′B′=2cm, \(\widehat {A'B'C'} = {70^o};\widehat {B'A'C'} = {80^o}\)(H.9.20b)
Em hãy dự đoán xem tam giác A'B'C' có đồng dạng với tam giác ABC không? nếu có thì tỉ số đồng dạng là bao nhiêu Phương pháp giải: Quan sát hình 9.20 để trả lời câu hỏi. Lời giải chi tiết: Tam giác A'B'C' đồng dạng với tam giác ABC với tỉ số đồng dạng \(\frac{1}{5}\) HĐ4 Video hướng dẫn giải Nếu ΔABC ∽ ΔA′B′C′ và anh Pi đo được A′C′=3,76cm thì khoảng cách từ bạn Tròn đến chân cột cờ là bao nhiêu mét? Phương pháp giải: Dựa vào tỉ số đồng dạng của hai tam giác, tính khoảng cách từ bạn Tròn đến chân cột cờ. Lời giải chi tiết: Có ΔA'B'C' ∽ ΔABC với tỉ số đồng dạng là \(\frac{1}{5}\) \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{1}{5}\) mà A′C′=3,76 (m) => AC=18,8 (m) Khoảng cách từ bạn Tròn đến chân cột cờ là 18,8 m. CH Video hướng dẫn giải Những cặp tam giác nào trong hình 9.22 là đồng dạng? Viết đúng kí hiệu đồng dạng
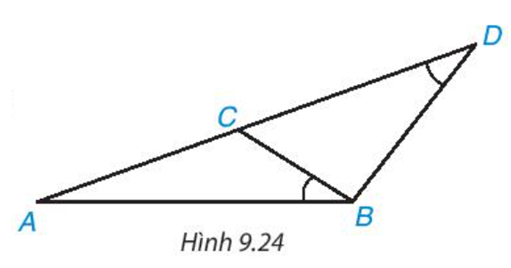
Phương pháp giải: Quan sát hình 9.22 và vận dụng trường hợp đồng dạng thứ ba của tam giác Lời giải chi tiết: Xét tam giác MPN có: \(\widehat P = {180^o} - \widehat M - \widehat N = {180^o} - {60^o} - {70^o} = {50^o}\) Các cặp tam giác đồng dạng trong hình 9.22 là: \(\Delta ACB \backsim \Delta DF{\rm{E; }}\Delta {\rm{ACB}} \backsim \Delta {\rm{MP}}N;\Delta DF{\rm{E}} \backsim \Delta MPN\) LT3 Video hướng dẫn giải Cho các điểm A, B, C, D như Hình 9.24. Biết rằng \(\widehat {ABC} = \widehat {A{\rm{D}}B}\). Hãy chứng minh ΔABC ∽ ΔADB và \(A{B^2} = A{\rm{D}}.AC\)
Phương pháp giải: Chứng minh ΔABC ∽ ΔADB (g.g) suy ra tỉ số đồng dạng Lời giải chi tiết: Xét tam giác ABC và tam giác ADB có \(\widehat {ABC} = \widehat {A{\rm{D}}B}\) và \(\widehat A\) chung => ΔABC ∽ ΔADB (g.g) => \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AB}}\) => \(A{B^2} = A{\rm{D}}.AC\) TTN Video hướng dẫn giải 1. Biết rằng ba đường phân giác của tam giác ABC đồng quy tại I, ba đường phân giác của tam giác A'B'C' đồng quy tại I'. Hãy chứng tỏ rằng nếu \( \widehat {A'I'B'} = \widehat {AIB} \) và \( \widehat {A'I'C'} = \widehat {AIC} \) thì \( \Delta A'B'C' \backsim \Delta ABC \). 2. Với hai tam giác ABC và A'B'C' trong phần Tranh luận, nếu thêm giả thiết các góc C và C' nhọn thì hai tam giác đó có đồng dạng không? Phương pháp giải: 1. Chứng minh tam giác ABC và tam giác A'B'C' đồng dạng theo trường hợp góc - góc. 2. Tương tự như phần Tranh luận, lấy điểm M trên tia BC sao cho \( \Delta ABM \backsim \Delta A'B'C' \). Giả sử điểm C không trùng với M và chứng minh điều đó là vô lý => Điểm C phải trùng với M và \( \Delta A'B'C' \backsim \Delta ABC \) Lời giải chi tiết: 1. Do tổng các góc trong một tam giác bằng $180^{\circ}$ nên: $\frac{\widehat{A^{\prime}}+\widehat{B^{\prime}}}{2}=180^{\circ}-\widehat{A^{\prime} I^{\prime} B^{\prime}}=180^{\circ}-\widehat{A I B}=\frac{\widehat{A}+\widehat{B}}{2} \text {. }$ Suy ra $\widehat{A^{\prime}}+\widehat{B^{\prime}}=\widehat{A}+\widehat{B}$. Do đó $\widehat{C^{\prime}}=180^{\circ}-\widehat{A^{\prime}}-\widehat{B^{\prime}}=180^{\circ}-\widehat{A}-\widehat{B}=\widehat{C} \text {. } $ Tương tự, $\widehat{B^{\prime}}=\widehat{B}$. Vậy $\triangle A^{\prime} B^{\prime} C^{\prime}$ và $\triangle A B C$ có: $\widehat{B^{\prime}}=\widehat{B}, \widehat{C^{\prime}}=\widehat{C}$. Do đó $\triangle A^{\prime} B^{\prime} C^{\prime} \backsim \triangle A B C$ (g.g). 2. Nếu góc C và C' đều nhọn: Lấy điểm $M$ trên tia $B C$ sao cho $\triangle A B M \perp \triangle A^{\prime} B^{\prime} C^{\prime}$. Giả sử điểm $C$ không trùng với $M$. Khi đó: $\triangle A^{\prime} B^{\prime} C^{\prime}$ và $\triangle A B M$ nên $\frac{A^{\prime} C^{\prime}}{A M}=\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} C^{\prime}}{A C}$ và kéo theo $A M=A C$, hay $\triangle A M C$ cân tại $A$. +) Nếu $M$ nằm giữa $B$ và $C$ thì $\widehat{A M B}=180^{\circ}-\widehat{A M C}$ $=180^{\circ}-\widehat{A C M}>90^{\circ}>\widehat{A^{\prime} C^{\prime} M^{\prime}}$ và ta nhận được điều vô lí. +) Vậy $C$ ở giữa $B$ và $M$ (như hình 9.19). Khi đó $\widehat{A C B}=180^{\circ}-\widehat{A C M}$ $=180^{\circ}-\widehat{A M B}=180^{\circ}-\widehat{C}>90^{\circ}$ và ta nhận được điều vô lí. Vậy điểm $C$ phải trùng với $M$ và $\triangle A^{\prime} B^{\prime} C^{\prime} \backsim \triangle A B C$.
|