Giải mục 3 trang 82, 83 SGK Toán 8 - Cùng khám phá1. Từ dấu hiệu nhận biết hình thoi, em hãy bổ sung thêm một điều kiện để một hình chữ nhật là hình vuông.
Lựa chọn câu để xem lời giải nhanh hơn
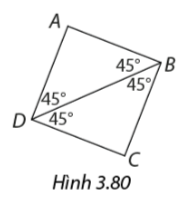
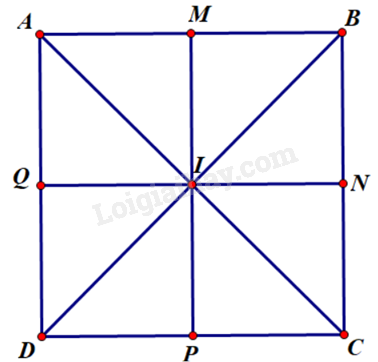
Hoạt động 3 1. Từ dấu hiệu nhận biết hình thoi, em hãy bổ sung thêm một điều kiện để một hình chữ nhật là hình vuông. 2. Từ dấu hiệu nhận biết hình chữ nhật, em hãy bổ sung một điều kiện để một hình thoi là hình vuông. Phương pháp giải: Dựa vào dấu hiệu nhận biết hình thoi, bổ sung thêm điều kiện để hình chữ nhật là hình vuông. Dựa vào dấu hiệu nhận biết hình chữ nhật, bổ sung thêm điều kiện để hình thoi là hình vuông. Lời giải chi tiết: 1. Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông; Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông. 2. Hình thoi có 1 góc vuông là hình vuông Hình thoi có hai đường chéo bằng nhau là hình vuông. Luyện tập 2 Tứ giác ABCD trong hình 3.80 có là hình vuông không? Vì sao? Phương pháp giải: Dựa vào dấu hiệu nhận biết hình vuông để xác định. Lời giải chi tiết: Xét tứ giác ABCD có \(AB//CD;AD//BC\) (có 1 cặp góc so le trong bằng nhau) Suy ra ABCD là hình bình hành. Có \(\widehat B = 45^\circ + 45^\circ = 90^\circ \) suy ra ABCD là hình chữ nhật (1) Xét tam giác ABD có \(\widehat B = \widehat D = 45^\circ \) nên tam giác ABD cân tại A \( \Rightarrow AD = AB\left( 2 \right)\) Từ (1) và (2) suy ra tứ giác ABCD là hình vuông. Vận dụng Một mặt bánh chưng có dạng hình vuông ABCD được cắt theo bốn đường thẳng \(AC,BD,MP,NQ\) trong đó \(M,N,P,Q\) lần lượt là trung điểm các cạnh \(AB,BC,CD,AD\)(hình 3.81). Vì sao bốn đường cắt này đồng quy? Phương pháp giải: Dựa vào tính chất của hình vuông và hình bình hành để chứng minh. Lời giải chi tiết:
Gọi I là trung điểm của AC suy ra AC và BD cắt nhau tại I (ABCD là hình vuông). (1) Xét tứ giác AMCP có \(AM//CP\left( {AB//CD} \right)\) và \(AM = CP\left( { = \frac{1}{2}AB = \frac{1}{2}CD} \right)\) Suy ra tứ giác AMCP là hình bình hành\( \Rightarrow \) AC và MP cắt nhau tại I (2) Xét tứ giác AQCN có \(AQ//NC\left( {AD//BC} \right)\) và \(AQ = NC\left( { = \frac{1}{2}AD = \frac{1}{2}CB} \right)\) Suy ra tứ giác AQCN là hình bình hành\( \Rightarrow \) AC và QN cắt nhau tại I (3) Từ (1); (2) và (3) suy ra \(AC,BD,MP,NQ\) đồng quy tại I.
|