Giải mục 3 trang 18, 19 Chuyên đề học tập Toán 11 - Kết nối tri thứcTrong hình 1.27, hãy chỉ ra ảnh của các điểm A, B, C, M, N, P qua phép quay tâm O, quay quay \(\pi \). Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh
Lựa chọn câu để xem lời giải nhanh hơn
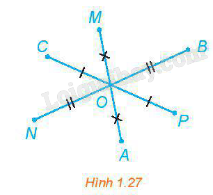
Hoạt động 3 Trong hình 1.27, hãy chỉ ra ảnh của các điểm A, B, C, M, N, P qua phép quay tâm O, quay quay \(\pi \).
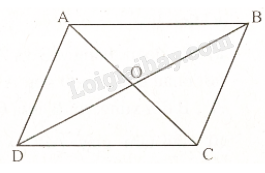
Phương pháp giải: Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay. Lời giải chi tiết: Ảnh của các điểm A, B, C, M, N, P qua phép quay tâm O, quay quay \(\pi \) lần lượt là M, N, P, A, B, C. Luyện tập 3 Cho hình hình hành ABCD có hai đường chéo cắt nhau tại O. Tìm ảnh của đường thẳng AB qua \(Đ_{O}\) Phương pháp giải: - Tìm ảnh của từng điểm A, B qua . Sau đó nối chúng với nhau ta được ảnh của AB qua \(Đ_{O}\) - Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \(Đ_{O}\). Điểm O được gọi là tâm đối xứng. Lời giải chi tiết:
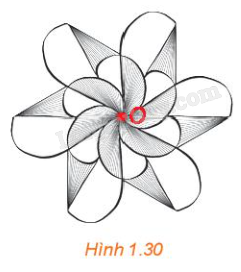
Vì ABCD là hình bình hành nên AC cắt BD tại O với O là trung điểm của AC và BD. Do đó, C là ảnh của A qua phép đối xứng tâm O; D là ảnh của B qua phép đối xứng tâm O. Vậy CD là ảnh của AB qua phép đối xứng tâm O. Vận dụng 2 Quan sát Hình 1.30, những phát biểu nào trong các phát biểu sau là đúng? a) Hình vẽ nhận điểm O (được tô đỏ) làm tâm đối xứng. b) Một đường thẳng bất kì đi qua điểm O sẽ chia hình vẽ thành hai nửa A và B giống nhau. Nếu thực hiện phép quay tâm O, góc quay 180∘ thì nửa A biến thành nửa B, tức là, B là ảnh của A qua một phép đối xứng tâm O. c) Có thể chia hình vẽ thành bốn phần giống nhau.
Phương pháp giải: Quan sát hình 1.30 và dựa vào kiến thức: Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu . Điểm O được gọi là tâm đối xứng. Lời giải chi tiết: Phát biểu a, b, c đều đúng.
|