Giải mục 2 trang 94, 95, 96 SGK Toán 11 tập 2 - Cùng khám phá

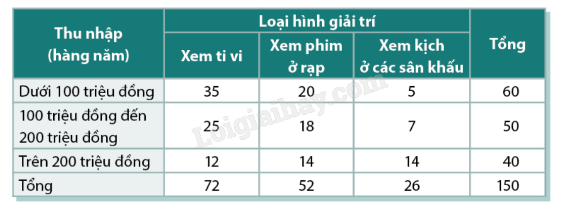
Hoạt động 2

Khánh và Hà mỗi người ném một quả bóng vào rổ. Xét các biến cố: 

M: "Không bạn nào ném bóng trúng vào rổ";

N: "Cả hai bạn đều ném bóng trúng vào rổ";

P: "Có đúng một bạn ném bóng trúng vào rổ";

Q: "Có ít nhất một bạn ném bóng trúng vào rồ".

a) Q có là biến cổ đối của M không?

b) Xác định biến cố \(N \cap P\).

c) N có biến cố đối của P hay không?

Phương pháp giải:

Cho A là một biến cố. Khi đó biến cố “Không xảy ra A” là biến cố đối của A.

Lời giải chi tiết:

a) Q là biến cố đối của M.

b) \(N \cap P = P\): “Có đúng một bạn ném bóng trúng vào rổ”

c) N không là là biến cố đối của P.

Luyện tập 2

Một hộp chứa bốn thẻ được đánh số 3, 4, 5, 6. Lấy ngẫu nhiên hai thẻ. Xét các biến cố:

A: "Tổng các số trên hai thẻ là số chẵn".

B: "Tích hai số trên hai thẻ là số chẵn";

C: "Tổng các số trên hai thẻ là số lẻ";

D: "Tích các số trên hai thẻ là số lẻ".

Hãy chỉ ra các cặp biến cố xung khắc trong các biến cố đã cho.

Phương pháp giải:

Hai biến cố xung khắc nếu chúng không đồng thời xảy ra.

Lời giải chi tiết:

A và C là hai biến cố xung khắc.

B và D là hai biến cố xung khắc.

Hoạt động 3

Cho A và B là hai biến cổ xung khắc liên quan đến một phép thử với không gian mẫu là \(\Omega \). Gọi \(n\left( A \right),n\left( B \right),n\left( {A \cup B} \right)\)và \(n\left( \Omega  \right)\) lần lượt là số phần tử của các biến cố A, B, \(A \cup B\) và không gian mẫu \(\Omega \).

a) Tìm \(n\left( {A \cup B} \right)\) theo \(n\left( A \right),n\left( B \right)\).

b) Viết công thức tính các xác suất P (A), P (B), \(P\left( {A \cup B} \right)\) theo \(n\left( A \right),n\left( B \right),n\left( {A \cup B} \right)\) và \(n\left( \Omega  \right)\).

c) Rút ra mối liên hệ giữa \(P\left( {A \cup B} \right)\) và P (A) + P (B).

Phương pháp giải:

Công thức xác suất: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\).

Lời giải chi tiết:

a) \(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right)\)

b) \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\)

\(P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega  \right)}}\)

\(P\left( {A \cup B} \right) = \frac{{n\left( {A \cup B} \right)}}{{n\left( \Omega  \right)}}\)

c) Ta có:

\(P\left( {A \cup B} \right) = \frac{{n\left( {A \cup B} \right)}}{{n\left( \Omega  \right)}} = \frac{{n\left( A \right) + n\left( B \right)}}{{n\left( \Omega  \right)}} = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}} + \frac{{n\left( B \right)}}{{n\left( \Omega  \right)}} = P\left( A \right) + P\left( B \right)\)

Luyện tập 3

Gieo hai con xúc xắc cân đối, đồng chất, có sáu mặt và quan sát tổng số chấm xuất hiện trên hai mặt. Tính xác suất để tổng số chấm xuất hiện ở hai mặt lớn hơn 5 và nhỏ hơn 8.

Phương pháp giải:

Công thức xác suất: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\).

Lời giải chi tiết:

\(n\left( \Omega  \right) = 36\)

Gọi A là biến cố “Tổng số chấm xuất hiện ở hai mặt lớn hơn 5 và nhỏ hơn 8”. Khi đó, \(n\left( A \right) = 5\)

\( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \frac{5}{{36}}\)

Hoạt động 4

Khánh chọn ngẫu nhiên một số từ 1 đến 10. Xét các biến cố:

A : "Số được chọn chia hết cho 2";

B : "Số được chọn chia hết cho 3".

a) Tính \(P\left( A \right),P\left( B \right),P\left( {A \cup B} \right),P\left( {A \cap B} \right)\).

b) So sánh \(P\left( {A \cup B} \right) + P\left( {A \cap B} \right)\) và \(P\left( A \right) + P\left( B \right)\).

Phương pháp giải:

Công thức xác suất: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\).

Lời giải chi tiết:

a)

\(\begin{array}{l}A = \left\{ {2;4;6;8;10} \right\} \Rightarrow n\left( A \right) = 5\\P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \frac{5}{{10}} = \frac{1}{2}\end{array}\)

\(\begin{array}{l}B = \left\{ {3;6;9} \right\} \Rightarrow n\left( B \right) = 3\\P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega  \right)}} = \frac{3}{{10}}\end{array}\)

\(\begin{array}{l}A \cup B = \left\{ {2;3;4;6;8;9;10} \right\} \Rightarrow n\left( {A \cup B} \right) = 7\\P\left( {A \cup B} \right) = \frac{{n\left( {A \cup B} \right)}}{{n\left( \Omega  \right)}} = \frac{7}{{10}}\end{array}\)

\(\begin{array}{l}A \cap B = \left\{ 6 \right\} \Rightarrow n\left( {A \cap B} \right) = 1\\P\left( {A \cap B} \right) = \frac{{n\left( {A \cap B} \right)}}{{n\left( \Omega  \right)}} = \frac{1}{{10}}\end{array}\)

b)

 \(\begin{array}{l}P\left( {A \cup B} \right) + P\left( {A \cap B} \right) = \frac{7}{{10}} + \frac{1}{{10}} = \frac{4}{5}\\P\left( A \right) + P\left( B \right) = \frac{1}{2} + \frac{3}{{10}} = \frac{4}{5}\\ \Rightarrow P\left( {A \cup B} \right) + P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right)\end{array}\)

Luyện tập 4

Bảng bên dưới cho kết quả khảo sát một nhóm gồm 150 người liên quan đến mức thu nhập (hàng năm) và loại hình giải trí mà họ yêu thích.

 

Chọn một người ngẫu nhiên trong nhóm khảo sát. Tính xác suất của các biến cố:

a) "Người được chọn thích xem kịch ở các sân khấu";

b) "Người được chọn có thu nhập trên 200 triệu"

c) "Người được chọn có thu nhập trên 200 triệu và thích xem kịch ở các sân khấu";

d ) "Người được chọn có thu nhập trên 200 triệu hoặc thích xem kịch ở các sân khấu".

Phương pháp giải:

Nếu A và B là hai biến cố bất kì liên quan đến một phép thử thì:

\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)\)

Lời giải chi tiết:

\(n\left( \Omega  \right) = 150\)

a) Gọi A là biến cố “Người được chọn thích xem kịch ở các sân khấu”

\(n\left( A \right) = 26\)

\( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \frac{{26}}{{150}} = \frac{{13}}{{75}}\)

b) Gọi B là biến cố "Người được chọn có thu nhập trên 200 triệu"

\(n\left( B \right) = 40\)

\( \Rightarrow P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega  \right)}} = \frac{{40}}{{150}} = \frac{4}{{15}}\)

c) Gọi C là biến cố “Người được chọn có thu nhập trên 200 triệu và thích xem kịch ở các sân khấu"

\(n\left( C \right) = 14\)

\( \Rightarrow P\left( C \right) = \frac{{n\left( C \right)}}{{n\left( \Omega  \right)}} = \frac{{14}}{{150}} = \frac{7}{{75}}\)

d) Gọi D là biến cố “Người được chọn có thu nhập trên 200 triệu hoặc thích xem kịch ở các sân khấu"

\( \Rightarrow P\left( D \right) = P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( C \right) = \frac{{26}}{{75}}\)