Giải mục 2 trang 85, 86, 87, 88, 89, 90 SGK Toán 11 tập 1 - Cùng khám pháTrong hình học phẳng, qua hai điểm phân biệt có thể xác định được bao nhiêu đường thẳng?
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 2 Trong hình học phẳng, qua hai điểm phân biệt có thể xác định được bao nhiêu đường thẳng? Phương pháp giải: Trong hình học phẳng, qua hai điểm phân biệt chỉ có thể xác định một đường thẳng. Lời giải chi tiết: Trong hình học phẳng, qua hai điểm phân biệt chỉ có thể xác định một đường thẳng. Hoạt động 3 a) Hãy sử dụng một giấy bìa cứng, vẽ và cắt thành hình một tam giác đều ABC như Hình 4.15. Lấy các điểm M, N, P lần lượt là trung điểm của AB, BC, CA, sau đó gấp lại theo các đường nét đứt MN, NP, PM và dán các mép với nhau bằng băng dính để được mô hình có hình biểu diễn như Hình 4.16. b) Sử dụng thêm một tấm bìa cứng phẳng (H), có thể đặt (H) chạm đồng thời vào bốn vị trí tương ứng với bốn điểm A, M, N, P hay không?
Phương pháp giải: Gấp hình theo hướng dẫn của đề bài để quan sát. Lời giải chi tiết: Không thể đặt (H) chạm đồng thời vào bốn vị trí tương ứng với bốn điểm A, M, N, P. Hoạt động 4 Vì sao người thợ xây thường dùng cây gỗ thẳng dài rê trên bề mặt sàn sau khi đổ bê tông? Vì sao người thợ mộc thường rê thước thẳng trên mặt bàn sau khi bào nhẵn mặt bàn (Hình 4.17)?
Phương pháp giải: Quan sát thực tế. Lời giải chi tiết: Người thợ xây thường dùng cây gỗ thẳng dài rê trên bề mặt sàn sau khi đổ bê tông và người thợ mộc thường rê thước thẳng trên mặt bàn sau khi bào nhẵn mặt bàn để xem mặt sàn, mặt bàn đã nhẵn và phẳng chưa. Luyện tập 3 Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC, BD. Khi đó, O và D có thuộc mặt phẳng (ABC) không? Phương pháp giải: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó. Lời giải chi tiết:
Ta thấy\(A,C \in \left( {ABC} \right)\). Mà \(O \in AC \Rightarrow O \in \left( {ABC} \right)\). Lại thấy \(O,B \in \left( {ABC} \right)\). Mà \(D \in OB \Rightarrow D \in \left( {ABC} \right)\). Hoạt động 5 a) Quan sát trong lớp học, xem mặt trường (có chứa bảng xanh) và sàn nhà là hình ảnh của hai mặt phẳng phân biệt (Hình 4.19). Hãy chỉ ra một số điểm chung của hai mặt phẳng này. b) Đặt quyển sách thẳng đứng trên mặt bàn và mở ra thành hai nửa (Hình 4.20). Xem hai trang giấy trước mặt là hình ảnh của hai mặt phẳng phân biệt (P), (Q). Hãy chỉ ra ít nhất ba điểm vừa thuộc (P) vừa thuộc (Q) và nhận xét về vị trí của các điểm này.
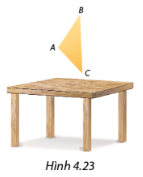
Phương pháp giải: Quan sát hình ảnh. Lời giải chi tiết: a) Các điểm chung của mặt tường và sàn nhà nằm trên đường chân tường. b) Các điểm vừa thuộc (P) vừa thuộc (Q) đều nằm trên cùng 1 đường thẳng chung của (P) và (Q) là gáy sách. Luyện tập 4 Bạn Nam cầm một miếng bìa hình tam giác với 3 đỉnh là A, B, C (Hình 4.23) đưa lên không quá cao so với mặt bàn và khẳng định rằng: “Nếu ta đặt các thanh thước dài dọc theo các cạnh AB, BC, CA để các thanh thước này chạm vào mặt bàn lần lượt tại các vị trí đánh dấu là điểm D, E, F thì ba điểm này thẳng hàng”. Bạn Mai không đồng ý và khẳng định: “D, E, F không thẳng hàng dược vì A, B, C không thẳng hàng”. Hãy cho biết ai đúng, ai sai? Vì sao?
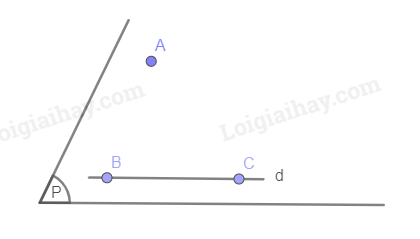
Phương pháp giải: Các điểm thuộc giao tuyến của 2 mặt phẳng phân biệt thì thẳng hàng. Lời giải chi tiết: Gọi mặt phẳng bàn là (Q). Theo đầu bài thì \(D,E,F \in \left( {ABC} \right)\) và \(\left( Q \right)\). Vậy ba điểm \(D,E,F\) cùng thuộc đường thẳng chung của \(\left( {ABC} \right)\) và \(\left( Q \right)\) nên \(D,E,F\) thẳng hàng. Hoạt động 6 a) Cho ba điểm A, B, C không thẳng hàng, một đường thẳng d đi qua hai điểm B, C. Hãy xác định một mặt phẳng chứa cả điểm A và đường thẳng d. b) Cho hai đường thẳng a, b cắt nhau tại điểm I. Trên các đường thẳng a, b lần lượt lấy các điểm A và B không trùng I. Các đường thẳng a, b có nằm trong mặt phẳng (ABI) hay không? Phương pháp giải: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó. Lời giải chi tiết: a)
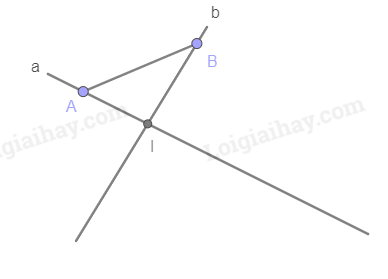
b)
\(A,I \in \left( {ABI} \right) \Rightarrow \)Đường thẳng a cũng thuộc mặt phẳng (ABI). \(B,I \in \left( {ABI} \right) \Rightarrow \) Đường thẳng b cũng thuộc mặt phẳng (ABI). Luyện tập 5 Trong mặt phẳng (P), cho tam giác ABC. Lấy S là điểm không thuộc mặt phẳng (P). Có hay không một mặt phẳng chứa cả hai đường thẳng SA và BC? Phương pháp giải: Chứng minh phản chứng: Giả sử tồn tại một mặt phẳng chứa 2 đường thẳng SA và BC. Chứng minh S không thuộc mặt phẳng đó. Lời giải chi tiết:
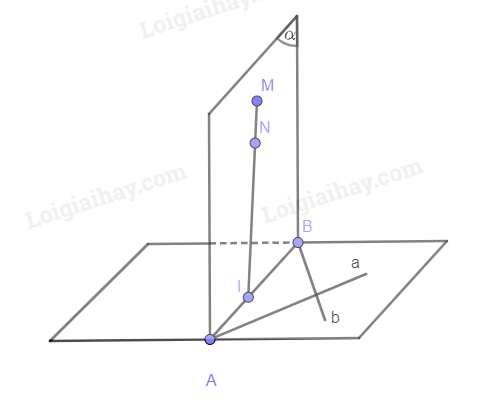
Giả sử có tồn tại mặt phẳng (Q) chứa 2 đường thẳng SA, BC. Khi đó S, A, B, C cùng thuộc mặt phẳng (Q). Ta có (Q) cũng chính là mặt phẳng (ABC). Suy ra S thuộc (ABC), mâu thuẫn với giả thiết S không thuộc (ABCD). Vậy không có mặt phẳng nào chứa cả hai đường thẳng SD và BC. Vận dụng 1 Cho hai đường thẳng a và b cắt nhau và hai điểm M, N không nằm trong mặt phẳng (a, b). Biết rằng đường thằng MN và mặt phẳng (a, b) luôn có một điểm chung. Một mặt phẳng \(\left( \alpha \right)\) thay đổi luôn luôn chứa MN và \(\left( \alpha \right)\) có điểm chung với hai đường thẳng a, b lần lượt là A, B. Chứng minh rằng dường thẳng AB luôn đi qua một điểm cố định khi \(\left( \alpha \right)\) thay đổi. Phương pháp giải: Nếu 2 mặt phẳng phân biệt có một điểm chung thì chúng có 1 đường thẳng chung duy nhất chứa tất cả các điểm chung của 2 mặt phẳng đó. Chứng minh AB luôn đi qua điểm chung đó. Lời giải chi tiết:
Gọi I là điểm chung của MN và mặt phẳng \(\left( {a,b} \right)\). Mặt phẳng \(\left( \alpha \right)\) và hai đường thẳng a, b có điểm chung là A, B \( \Rightarrow \left( \alpha \right) \cap \left( {a,b} \right) = AB\) Mà: \(MN \in \left( \alpha \right)\) Nên \(I \in AB\) Vì MN và \(\left( {a,b} \right)\) không thay đổi nên I không thay đổi. Vậy đường thẳng AB luôn đi qua một điểm cố định khi \(\left( \alpha \right)\) thay đổi.
|