Giải mục 2 trang 79, 80 SGK Toán 8 tập 1 - Kết nối tri thức

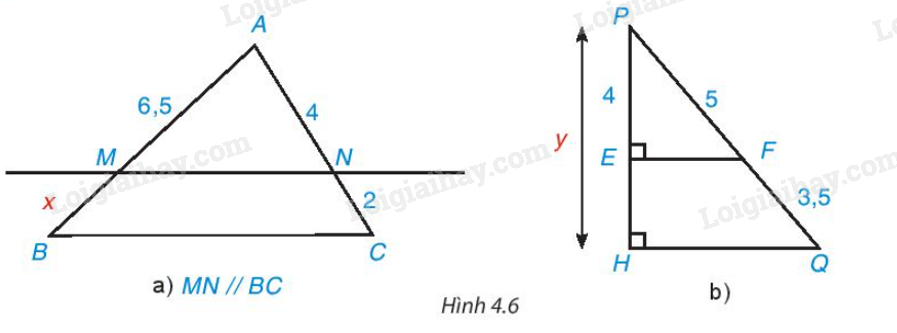
Luyện tập 3

Tìm các độ dài x, y trong Hình 4.6.

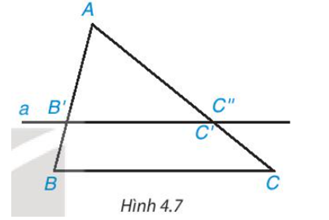
Phương pháp giải:

Áp dụng định lí Thalès

Lời giải chi tiết:

a) Áp dụng định lí Thalès vào ∆ABC, ta có:

\(\dfrac{{AM}}{{BM}} = \dfrac{{AN}}{{CN}}\) hay \(\dfrac{{6,5}}{x} = \dfrac{4}{2}\)

Suy ra \(x = \dfrac{{6,5.2}}{4} = 3,25\) (đvđd).

Vậy x = 3,25 (đvđd).

b) Ta có: PQ = PF + QF = 5 + 3,5 = 8,5 (đvđd).

Áp dụng định lí Thalès vào ∆PHQ, ta có:

\(\dfrac{{PE}}{{PH}} = \dfrac{{PF}}{{PQ}}\) hay \(\dfrac{4}{y} = \dfrac{5}{{8,5}}\)

Suy ra \(y = \dfrac{{4.8,5}}{5} = 6,8\) (đvđd).

Vậy y = 6,8 (đvđd)

HĐ 4

Cho ∆ABC có AB = 6 cm, AC = 9 cm. Trên cạnh AB lấy điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 4 cm, AC’ = 6 cm (H.4.7).

• So sánh các tỉ số \(\dfrac{{AB'}}{{AB}}\) và \(\dfrac{{AC'}}{{AC}}\)

• Vẽ đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’. Tính độ dài đoạn thẳng AC’’.

• Nhận xét gì về hai điểm C’, C’’ và hai đường thẳng B’C’, BC?

Phương pháp giải:

Áp dụng định lí Thalès vào ∆ABC

Lời giải chi tiết:

• Ta có \(\dfrac{{AB'}}{{AB}} = \dfrac{4}{6} = \dfrac{2}{3};\dfrac{{AC'}}{{AC}} = \dfrac{6}{9} = \dfrac{2}{3}\)

Do đó \(\dfrac{{AB'}}{{AB}} = \dfrac{{AC'}}{{AC}}\)

• Đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’ nên B’C’’ // BC.

Áp dụng định lí Thalès vào ∆ABC, ta có:

\(\dfrac{{AB'}}{{AB}} = \dfrac{{AC''}}{{AC}}\) hay \(\dfrac{4}{6} = \dfrac{{AC''}}{9}\)

Suy ra: \(AC'' = \dfrac{{4.9}}{6} = 6\)(cm).

Vậy AC’’ = 6 cm.

• Trên cạnh AC lấy điểm C’ sao cho AC’ = 6 cm.

Đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’ nên điểm C’’ nằm trên cạnh AC sao cho AC’’ = 6 cm.

Do đó, hai điểm C’, C’’ trùng nhau.

Vì hai điểm C’, C’’ trùng nhau mà B’C’’ // BC nên B’C’ // BC.

Vận dụng

Cây cầu AB bắc qua một con sông có chiều rộng 300 m. Để đo khoảng cách giữa hai điểm C và D trên hai bờ con sông, người ta chọn một điểm E trên đường thẳng AB sao cho ba điểm E, C, D thẳng hàng. Trên mặt đất, người ta đo được AE = 400 m, EC = 500 m. Theo em, người ta tính khoảng cách giữa C và D như thế nào?

Phương pháp giải:

Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès

Lời giải chi tiết:

Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès, ta có:

 \(\dfrac{{A{\rm{E}}}}{{AB}} = \dfrac{{CE}}{{C{\rm{D}}}}\) hay \(\dfrac{{400}}{{300}} = \dfrac{{500}}{{C{\rm{D}}}}\)

Suy ra \(C{\rm{D}} = \dfrac{{300.500}}{{400}} = 375\) (m).

Vậy khoảng cách giữa C và D bằng 375 m