Giải mục 2 trang 74, 75 SGK Toán 8 tập 2– Chân trời sáng tạoCho hai tam giác vuông Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên
Lựa chọn câu để xem lời giải nhanh hơn
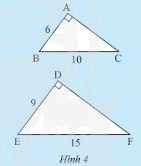
HĐ2 Video hướng dẫn giải Cho hai tam giác vuông \(ABC\) và \(DEF\) có các kích thước như Hình 4. a) Hãy tính độ dài cạnh \(AC\) và \(DF\). b) So sánh các tỉ số \(\frac{{AB}}{{DE}};\frac{{AC}}{{DF}}\) và \(\frac{{BC}}{{EF}}\). c) Dự đoán sự đồng dạng của hai tam giác\(ABC\) và \(DEF\).
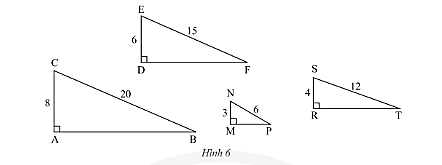
Phương pháp giải: - Sử dụng định lí Py – ta – go. - Chứng minh tam giác đồng dạng theo trường hợp cạnh – cạnh – cạnh Lời giải chi tiết: a) Xét tam giác \(ABC\) vuông tại \(A\) ta có: \(A{B^2} + A{C^2} = B{C^2}\) (định lí Py – ta – go) \( \Leftrightarrow {6^2} + A{C^2} = {10^2} \Leftrightarrow A{C^2} = {10^2} - {6^2} = 64 \Leftrightarrow AC = 8\). Xét tam giác \(DEF\) vuông tại \(D\) ta có: \(D{E^2} + D{F^2} = E{F^2}\) (định lí Py – ta – go) \( \Leftrightarrow {9^2} + D{F^2} = {15^2} \Leftrightarrow D{F^2} = {15^2} - {9^2} = 144 \Leftrightarrow DF = 12\). b) Tỉ số: \(\frac{{AB}}{{DE}} = \frac{6}{9} = \frac{2}{3};\frac{{AC}}{{DF}} = \frac{8}{{12}} = \frac{2}{3}\); \(\frac{{BC}}{{EF}} = \frac{{10}}{{15}} = \frac{2}{3}\). Do đó, \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\). c) Xét tam giác\(ABC\) và tam giác\(DEF\) có: \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\) (chứng minh trên) Do đó, \(\Delta ABC\backsim\Delta DEF\) (c.c.c) TH2 Video hướng dẫn giải Trong Hình 6, tam giác nào đồng dạng với tam giác \(DEF\)?
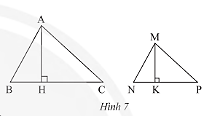
Phương pháp giải: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau. Lời giải chi tiết: Tỉ số: \(\frac{{DE}}{{AC}} = \frac{6}{8} = \frac{3}{4};\frac{{EF}}{{BC}} = \frac{{15}}{{20}} = \frac{3}{4}\). Xét tam giác\(DEF\) và tam giác\(ABC\) có: \(\frac{{DE}}{{AC}} = \frac{{EF}}{{BC}} = \frac{3}{4}\) (chứng minh trên) Do đó, \(\Delta DEF\backsim\Delta ABC\). Tỉ số: \(\frac{{DE}}{{MN}} = \frac{6}{3} = 2;\frac{{EF}}{{NP}} = \frac{{15}}{6} = \frac{5}{2}\). Vì \(\frac{{DE}}{{MN}} \ne \frac{{EF}}{{NP}}\) nên hai tam giác \(DEF\) và \(MNP\) không đồng dạng với nhau. Tỉ số: \(\frac{{DE}}{{RS}} = \frac{6}{4} = \frac{3}{2};\frac{{EF}}{{ST}} = \frac{{15}}{{12}} = \frac{5}{4}\). Vì \(\frac{{DE}}{{RS}} \ne \frac{{EF}}{{ST}}\) nên hai tam giác \(DEF\) và \(SRT\) không đồng dạng với nhau. VD2 Video hướng dẫn giải Trong Hình 7, biết \(\Delta MNP\backsim\Delta ABC\) với tỉ số đồng dạng \(k = \frac{{MN}}{{AB}}\), hai đường cao tương ứng là \(MK\) và \(AH\). a) Chứng minh rằng \(\Delta MNK\backsim\Delta ABH\)và \(\frac{{MK}}{{AH}} = k\). b) Gọi \({S_1}\) là diện tích tam giác \(MNP\) và \({S_2}\) là diện tích tam giác \(ABC\). Chứng minh rằng \(\frac{{{S_1}}}{{{S_2}}} = {k^2}\).
Phương pháp giải: - Nếu một tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau. - Diện tích tam giác vuông bằng một nửa tích hai cạnh góc vuông. Lời giải chi tiết: a) Vì tam giác \(\Delta MNP\backsim\Delta ABC\) nên \(\widehat B = \widehat N\) (hai góc tương ứng). Vì \(MK\) là đường cao nên \(\widehat {MKN} = 90^\circ \);Vì \(AH\) là đường cao nên \(\widehat {AHB} = 90^\circ \) Xét \(\Delta MNK\) và \(\Delta ABH\) có: \(\widehat B = \widehat N\) (chứng minh trên) \(\widehat {MKN} = \widehat {AHB} = 90^\circ \) Do đó, \(\Delta MNK\backsim\Delta ABH\) (g.g) Vì \(\Delta MNK\backsim\Delta ABH\) nên ta có: \(\frac{{MN}}{{AB}} = \frac{{NK}}{{BH}} = \frac{{MK}}{{AH}} = k \Rightarrow \frac{{MK}}{{AH}} = k\). b) Vì \(\Delta MNP\backsim\Delta ABC\) nên \(\frac{{MN}}{{AB}} = \frac{{NP}}{{BC}} = \frac{{MP}}{{AC}} = k\) \( \Rightarrow \frac{{NP}}{{BC}} = k \Leftrightarrow NP = kBC\) Vì \(\frac{{MK}}{{AH}} = k \Rightarrow MK = kAH\) Diện tích tam giác \(MNP\) là: \({S_1} = \frac{1}{2}.MK.NP\) (đvdt) Diện tích tam giác \(ABC\) là: \({S_2} = \frac{1}{2}.AH.BC\) (đvdt) Ta có: \(\frac{{{S_1}}}{{{S_2}}} = \frac{{\frac{1}{2}.MK.NP}}{{\frac{1}{2}.AH.BC}} = \frac{{kAH.kBC}}{{AH.BC}} = {k^2}\) (điều phải chứng minh)
|