Giải mục 2 trang 65, 66 SGK Toán 8 tập 1 - Kết nối tri thức

HĐ3

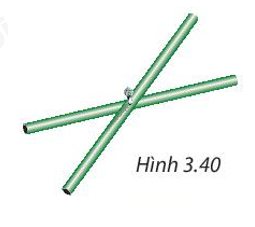
Cho hình bình hành ABCD có góc A vuông. Tính các góc B, C, D. Tứ giác ABCD có là hình chữ nhật không? Vì sao?

Phương pháp giải:

Sử dụng định lí tổng ba góc của một tứ giác.

Lời giải chi tiết:

Vì ABCD là hình bình hành nên $\widehat A = \widehat C;\widehat B = \widehat D$

Suy ra $\widehat A = \widehat C = {90^o}$

Ta có $\widehat A + \widehat B + \widehat C + \widehat D = {360^o}$

 90°+$\widehat B$+90°+$\widehat B$=360°

 2$\widehat B$+180°=360°

Suy ra 2$\widehat B$=360°−180°=180°

Mà $\widehat B = \widehat D$ nên $\widehat B = \widehat D = {90^o}$

Do đó $\widehat B = \widehat C = \widehat D = {90^o}$

Hình bình hành ABCD là hình chữ nhật vì $\widehat A = \widehat B = \widehat C = \widehat D = {90^o}$

Luyện tập 2

Cho tứ giác ABCD có $\widehat A = {90^o}$,  hai đường chéo cắt nhau tại trung điểm O của mỗi đường. Hỏi tứ giác ABCD là hình gì? Tại sao?

Phương pháp giải:

Chứng minh tứ giác ABCD là hình bình hành có $\widehat A = {90^o}$nên ABCD là hình chữ nhật

Lời giải chi tiết:

Tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm O của mỗi đường nên tứ giác ABCD là hình bình hành.

Hình bình hành ABCD là có $\widehat A = {90^o}$

Do đó, tứ giác ABCD là hình chữ nhật.

Vận dụng

Hai thanh tre thẳng bằng nhau, được gắn với nhau tại trung điểm của mỗi thanh. Khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác (H.3.40) thì tứ giác đó là hình gì? Tại sao?

Phương pháp giải:

Nhận xét về hai thanh tre tạo thành hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

Lời giải chi tiết:

Hai đầu mút của hai thanh tre tạo thành bốn đỉnh của tứ giác.

Tứ giác đó có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên tứ giác đó là hình chữ nhật.

Vậy khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác thì tứ giác đó là hình chữ nhật.