Giải mục 2 trang 65, 66 SGK Toán 8 – Chân trời sáng tạo

HĐ 3

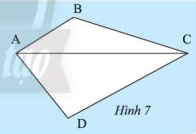
Đường chéo $AC$ chia tứ giác $ABCD$ thành hai tam giác $ACB$ và $ACD$ (Hình 7). Tính tổng các góc của tam giác $ACB$ và tam giác $ACD$. Từ đó, ta có nhận xét gì về tổng các góc của tứ giác $ABCD$ .

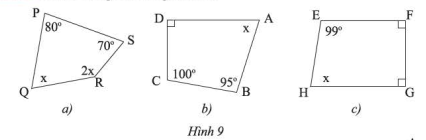
Phương pháp giải:

Sử dụng tính chất: Tổng ba góc trong một tam giác bằng $180^\circ$

Lời giải chi tiết:

Xét $\Delta ABC$ ta có:

$\widehat B + \widehat {BAC} + \widehat {BCA} = 180^\circ$ (tính chất tổng ba góc trong tam giác)

Xét $\Delta DAC$ ta có:

$\widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ$

Ta có:

$\widehat B + \widehat {BAC} + \widehat {BCA} + \widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ  + 180^\circ$

$\widehat B + \widehat D + \left( {\widehat {BAC} + \widehat {DAC}} \right) + \left( {\widehat {BCA} + \widehat {DCA}} \right) = 360^\circ$

$\widehat B + \widehat D + \widehat {BAD} + \widehat {BCD} = 360^\circ$

Vậy tổng các góc của tứ giác $ABCD$ bằng $360^\circ$

TH 2

Tìm $x$ trong mỗi tứ giác sau:

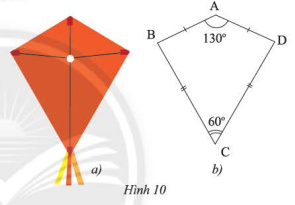
Phương pháp giải:

Sử dụng tính chất: Tổng các góc trong một tứ giác bằng $360^\circ$

Lời giải chi tiết:

Do tổng số đo bốn góc của một tứ giác bằng $360^\circ$ nên ta có:

a) Trong tứ giác $PQRS$:

$x + 2x = 360^\circ  - \left( {80^\circ  + 70^\circ } \right) = 210^\circ$

$3x = 210^\circ$

$x = 70^\circ$

b) Trong tứ giác $ABCD$:

$x = 360^\circ  - \left( {90^\circ  + 100^\circ  + 95^\circ } \right)$

$x = 75^\circ$

c) Trong tứ giác $EFGH$:

$x = 360^\circ  - \left( {99^\circ  + 90^\circ  + 90^\circ } \right)$

$x = 81^\circ$

VD 2

Phần thân của cái diều ở Hình 10a được vẽ lại như Hình 10b. Tìm số đo các góc chưa biết trong hình.

Phương pháp giải:

Sử dụng tính chất: Tổng các góc trong một tứ giác bằng $360^\circ$

Lời giải chi tiết:

Do tổng số đo bốn góc của một tứ giác bằng $360^\circ$ nên ta có:

$\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ$

$130^\circ  + \widehat B + 60^\circ  + \widehat D = 360^\circ$

$\widehat B + \widehat D = 170^\circ$ (1)

Xét $\Delta ABC$ và $\Delta ADC$ ta có:

$AB = AD$ (gt)

$BC = DC$ (gt)

$AC$ chung

$\Rightarrow \Delta ABC = \Delta ADC$ (c-c-c)

$\Rightarrow \widehat B = \widehat D$ (hai góc tương ứng) (2)

Từ (1) và (2) suy ra: $\widehat B = \widehat D = \frac{{170^\circ }}{2} = 85^\circ$