Giải mục 2 trang 6, 7, 8 Chuyên đề học tập Toán 11 - Kết nối tri thứcTrên mặt phẳng tọa độ Oxy, cho phép biến hình f biến mỗi điểm (Mleft( {x;{rm{ }}y} right)) thành điểm (M'left( {x{rm{ }} + {rm{ }}1;{rm{ }}y{rm{ }} + {rm{ }}2} right).) Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh
Lựa chọn câu để xem lời giải nhanh hơn
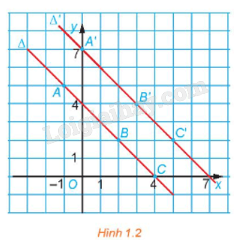
Hoạt động 2 Trên mặt phẳng tọa độ Oxy, cho phép biến hình f biến mỗi điểm \(M\left( {x;{\rm{ }}y} \right)\) thành điểm \(M'\left( {x{\rm{ }} + {\rm{ }}1;{\rm{ }}y{\rm{ }} + {\rm{ }}2} \right).\) a) Xét các điểm \(A\left( {-{\rm{ }}1;{\rm{ }}5} \right),{\rm{ }}B\left( {2;{\rm{ }}2} \right),{\rm{ }}C\left( {4;{\rm{ }}0} \right)\) thuộc \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\). Xác định các ảnh của chúng qua f. b) Chứng minh rằng nếu \(M\left( {{x_0};{\rm{ }}{y_0}} \right)\) là điểm thuộc đường thẳng \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\) thì ảnh \(M'\left( {{x_0}\; + {\rm{ }}1;{\rm{ }}{y_0}\; + {\rm{ }}2} \right)\) của nó thuộc đường thẳng \(\Delta ':{\rm{ }}x + {\rm{ }}y{\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0.\;\;\)
Phương pháp giải: Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\). Lời giải chi tiết: a) Ảnh của điểm A(– 1; 5) qua phép biến hình f là điểm \(A'\left( {-{\rm{ }}1{\rm{ }} + {\rm{ }}1;{\rm{ }}5{\rm{ }} + {\rm{ }}2} \right)\) hay \(A'\left( {0;{\rm{ }}7} \right).\) Ảnh của điểm B(2; 3) qua phép biến hình f là điểm \(B'\left( {2{\rm{ }} + {\rm{ }}1;{\rm{ }}3{\rm{ }} + {\rm{ }}2} \right)\) hay \(B'\left( {3;{\rm{ }}5} \right).\) Ảnh của điểm C(4; 0) qua phép biến hình f là điểm \(C'\left( {4{\rm{ }} + {\rm{ }}1;{\rm{ }}0{\rm{ }} + {\rm{ }}2} \right)\) hay \(C'\left( {5;{\rm{ }}2} \right).\) b) Vì \(M\left( {{x_0};{\rm{ }}{y_0}} \right)\) thuộc \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\) nên \({x_0}\; + {\rm{ }}{y_0}\;-{\rm{ }}4{\rm{ }} = {\rm{ }}0\) hay \({x_0}\; + {\rm{ }}{y_{0\;}} = {\rm{ }}4\) \(\begin{array}{*{20}{l}}{ \Leftrightarrow \;{x_0}\; + {\rm{ }}{y_0}\; + {\rm{ }}3{\rm{ }} = {\rm{ }}4{\rm{ }} + {\rm{ }}3}\\{ \Leftrightarrow \;\left( {{x_0}\; + {\rm{ }}1} \right){\rm{ }} + {\rm{ }}\left( {{y_{0\;}} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }}7}\\{ \Leftrightarrow \;\left( {{x_0}\; + {\rm{ }}1} \right){\rm{ }} + {\rm{ }}\left( {{y_{0\;}} + {\rm{ }}2} \right){\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0}\end{array}\) Suy ra \(M'\left( {{x_0}\; + {\rm{ }}1;{\rm{ }}{y_0}\; + {\rm{ }}2} \right)\) thuộc đường thẳng \(\Delta ':{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0.\) Vận dụng 1 Quan sát ba tấm ảnh hoa hồng ở Hình 1.4, hãy cho biết hình nào giống ảnh của hình ở giữa qua một phép co về trục.
Phương pháp giải: Quan sát hình vẽ để trả lời Lời giải chi tiết: Quan sát Hình 1.4, ta thấy hình phía bên phải hình ở giữa giống ảnh của hình ở giữa qua một phép co về trục.
|