Giải mục 2 trang 57, 58, 59 SGK Toán 10 tập 1 - Kết nối tri thức

HĐ3

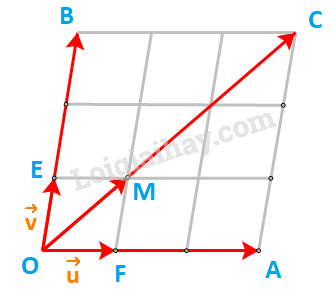
Với $\overrightarrow u  \ne \overrightarrow 0$ và hai số thực k, t, những khẳng định nào sau đây là đúng?

a) Hai vecto $k\left( {t\overrightarrow u } \right)$ và $\left( {kt} \right)\overrightarrow u$ có cùng độ dài bằng $\left| {kt} \right|.\left| {\overrightarrow u } \right|$

b) Nếu $kt \ge 0$ thì cả hai vecto $k\left( {t\overrightarrow u } \right)$, $\left( {kt} \right)\overrightarrow u$ cùng hướng với $\overrightarrow u$

c) Nếu $kt < 0$ thì cả hai vecto $k\left( {t\overrightarrow u } \right)$, $\left( {kt} \right)\overrightarrow u$ ngược hướng với $\overrightarrow u$

d) Hai vecto $k\left( {t\overrightarrow u } \right)$ và $\left( {kt} \right)\overrightarrow u$ bằng nhau.

Phương pháp giải:

Vecto $k\;\overrightarrow a$ (với $k > 0,\;\overrightarrow a  \ne \overrightarrow 0$)  cùng hướng với vecto $\overrightarrow a$ và có độ đài bằng $k\;\left| {\overrightarrow a } \right|$.

Vecto $k\;\overrightarrow a$ (với $k < 0,\;\overrightarrow a  \ne \overrightarrow 0$)  ngược hướng với vecto $\overrightarrow a$ và có độ đài bằng $\left| k \right|\;\left| {\overrightarrow a } \right|$.

Lời giải chi tiết:

a) Hai vecto $k\left( {t\overrightarrow u } \right)$ và $\left( {kt} \right)\overrightarrow u$ có cùng độ dài bằng $\left| {kt} \right|.\left| {\overrightarrow u } \right|$

Ta có: $\left| {t\overrightarrow u } \right| = \left| t \right|\left| {\overrightarrow u } \right| \Rightarrow \left| {k\left( {t\overrightarrow u } \right)} \right| = \left| k \right|\left| {\left( {t\overrightarrow u } \right)} \right| = \left| k \right|.\left| t \right|\left| {\overrightarrow u } \right| = \left| {kt} \right|\left| {\overrightarrow u } \right|$

Và $\left| {\left( {kt} \right)\overrightarrow u } \right| = \left| {kt} \right|\left| {\overrightarrow u } \right|$

$\Rightarrow \left| {k\left( {t\overrightarrow u } \right)} \right| = \left| {\left( {kt} \right)\overrightarrow u } \right| = \left| {kt} \right|\left| {\overrightarrow u } \right|$

b) Nếu $kt \ge 0$ thì cả hai vecto $k\left( {t\overrightarrow u } \right)$, $\left( {kt} \right)\overrightarrow u$ cùng hướng với $\overrightarrow u$

Ta xét 2 trường hợp:

Trường hợp 1: $k \ge 0,t \ge 0$

Vecto $k\left( {t\overrightarrow u } \right)$ cùng hướng với vecto $t\overrightarrow u$ (vì $k \ge 0$ ), mà vecto $t\overrightarrow u$ cùng hướng với vecto $\overrightarrow u$ (vì $t \ge 0$ )

Do đó vecto $k\left( {t\overrightarrow u } \right)$ cùng hướng với vecto $\overrightarrow u$.

Trường hợp 2: $k < 0,t < 0$

Vecto $k\left( {t\overrightarrow u } \right)$ ngược hướng với vecto $t\overrightarrow u$ (vì $k < 0$ ), mà vecto $t\overrightarrow u$ ngược hướng với vecto $\overrightarrow u$ (vì $t < 0$ )

Do đó vecto $k\left( {t\overrightarrow u } \right)$ cùng hướng với vecto $\overrightarrow u$.

Vậy vecto $k\left( {t\overrightarrow u } \right)$ luôn cùng hướng với vecto $\overrightarrow u$ nếu $kt \ge 0$.

Lại có: $kt \ge 0$ nên $\left( {kt} \right)\overrightarrow u$ cùng hướng với $\overrightarrow u$

Vậy $kt \ge 0$ thì cả hai vecto $k\left( {t\overrightarrow u } \right)$, $\left( {kt} \right)\overrightarrow u$ cùng hướng với $\overrightarrow u$

c) Nếu $kt < 0$ thì cả hai vecto $k\left( {t\overrightarrow u } \right)$, $\left( {kt} \right)\overrightarrow u$ ngược hướng với $\overrightarrow u$

Ta xét 2 trường hợp:

Trường hợp 1: $k > 0,t < 0$

Vecto $k\left( {t\overrightarrow u } \right)$ cùng hướng với vecto $t\overrightarrow u$ (vì $k > 0$ ), mà vecto $t\overrightarrow u$ ngược hướng với vecto $\overrightarrow u$ (vì $t < 0$)

Do đó vecto $k\left( {t\overrightarrow u } \right)$ ngược hướng với vecto $\overrightarrow u$.

Trường hợp 2: $k < 0,t > 0$

Vecto $k\left( {t\overrightarrow u } \right)$ ngược hướng với vecto $t\overrightarrow u$ (vì $k < 0$ ), mà vecto $t\overrightarrow u$ cùng hướng với vecto $\overrightarrow u$ (vì $t > 0$)

Do đó vecto $k\left( {t\overrightarrow u } \right)$ ngược hướng với vecto $\overrightarrow u$.

Vậy vecto $k\left( {t\overrightarrow u } \right)$ luôn ngược hướng với vecto $\overrightarrow u$ nếu $kt < 0$.

Lại có: $kt < 0$ nên $\left( {kt} \right)\overrightarrow u$ ngược hướng với $\overrightarrow u$

Vậy $kt < 0$ thì cả hai vecto $k\left( {t\overrightarrow u } \right)$, $\left( {kt} \right)\overrightarrow u$ ngược hướng với $\overrightarrow u$

d)

Từ ý b) và c), ra suy ra hai vecto $k\left( {t\overrightarrow u } \right)$ và $\left( {kt} \right)\overrightarrow u$luôn cùng hướng.

Theo câu a) ta có: $\left| {k\left( {t\overrightarrow u } \right)} \right| = \left| {\left( {kt} \right)\overrightarrow u } \right| = \left| {kt} \right|\left| {\overrightarrow u } \right|$

$\Rightarrow$  Hai vecto $k\left( {t\overrightarrow u } \right)$ và $\left( {kt} \right)\overrightarrow u$ bằng nhau

HĐ4

Hãy chỉ ra trên Hình 4.26 hai vecto $3\left( {\overrightarrow u  + \overrightarrow v } \right)$ và $3\overrightarrow u  + 3\overrightarrow v$. Từ đó, nêu mối quan hệ giữa $3\left( {\overrightarrow u  + \overrightarrow v } \right)$ và $3\overrightarrow u  + 3\overrightarrow v$

Lời giải chi tiết:

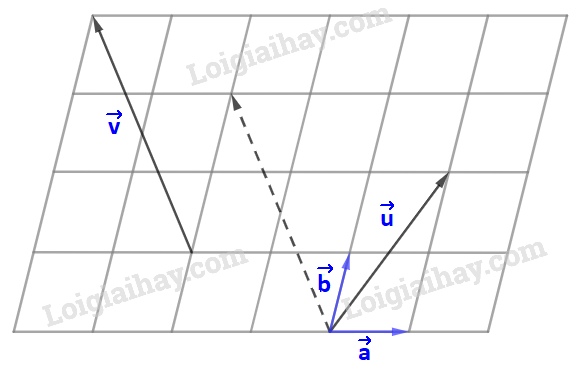
Kí hiệu O, E, F là các điểm như trên hình vẽ.

Dễ thấy: tứ giác OEMF là hình bình hành nên $\overrightarrow {OE}  + \overrightarrow {OF}  = \overrightarrow {OM}$ hay $\overrightarrow v  + \overrightarrow u  = \overrightarrow {OM}$

Và $\overrightarrow {OC}  = 3.\overrightarrow {OM}  \Rightarrow 3\left( {\overrightarrow v  + \overrightarrow u } \right) = 3.\overrightarrow {OM}  = \overrightarrow {OC}$

Mặt khác: $\overrightarrow {OA}  = 3.\overrightarrow {OF}  = 3\;\overrightarrow u ;\;\overrightarrow {OB}  = 3.\overrightarrow {OE}  = 3\;\overrightarrow v$

Và $\overrightarrow {OB}  + \overrightarrow {OA}  = \overrightarrow {OC}$ hay $3\;\overrightarrow v  + 3\;\overrightarrow u  = \overrightarrow {OC}$

$\Rightarrow 3\left( {\overrightarrow v  + \overrightarrow u } \right) = 3\;\overrightarrow v  + 3\;\overrightarrow u$

Luyện tập 2

Cho tam giác ABC có trọng tâm G. Chứng minh rằng với điểm O tùy ý, ta có

$\overrightarrow {OB}  + \overrightarrow {OA}  + \overrightarrow {OC}  = 3\overrightarrow {OG}$.

Phương pháp giải:

G là trọng tâm của tam giác ABC thì $\overrightarrow {GB}  + \overrightarrow {GA}  + \overrightarrow {GC}  = \overrightarrow 0$

Với 3 điểm A, B, C bất kì, ta luôn có $\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC}$

Lời giải chi tiết:

Ta có: $\overrightarrow {OA}  = \overrightarrow {OG}  + \overrightarrow {GA}$; $\overrightarrow {OB}  = \overrightarrow {OG}  + \overrightarrow {GB}$; $\overrightarrow {OC}  = \overrightarrow {OG}  + \overrightarrow {GC}$

$\begin{array}{l} \Rightarrow \overrightarrow {OB}  + \overrightarrow {OA}  + \overrightarrow {OC}  = \overrightarrow {OG}  + \overrightarrow {GA}  + \overrightarrow {OG}  + \overrightarrow {GB}  + \overrightarrow {OG}  + \overrightarrow {GC} \\ \Leftrightarrow \overrightarrow {OB}  + \overrightarrow {OA}  + \overrightarrow {OC}  = 3\overrightarrow {OG}  + \left( {\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC} } \right)\end{array}$

Do G là trọng tâm của tam giác ABC nên $\overrightarrow {GB}  + \overrightarrow {GA}  + \overrightarrow {GC}  = \overrightarrow 0$

$\begin{array}{l} \Rightarrow \overrightarrow {OB}  + \overrightarrow {OA}  + \overrightarrow {OC}  = 3\overrightarrow {OG}  + \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {OB}  + \overrightarrow {OA}  + \overrightarrow {OC}  = 3\overrightarrow {OG} \end{array}$

Luyện tập 3

Trong hình 4.27, hãy biểu thị mỗi vecto $\overrightarrow u ,\;\overrightarrow v$ theo hai vecto $\overrightarrow a ,\;\overrightarrow b$, tức là tìm các số $x,y,z,t$ để $\overrightarrow u  = x\overrightarrow a  + y\overrightarrow b ,\;\overrightarrow v  = t\overrightarrow a  + z\overrightarrow b .$.

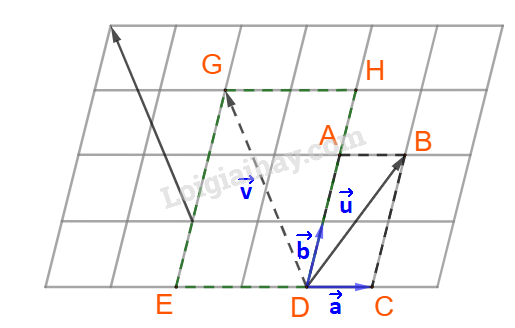
Phương pháp giải:

Phân tích vecto $\overrightarrow u ,\;\overrightarrow v$ theo hai vecto $\overrightarrow a ,\;\overrightarrow b$ cho trước.

Lời giải chi tiết:

Bước 1: Dựng hình bình hành có cạnh song song với giá của vecto $\overrightarrow a ,\;\overrightarrow b$ và đường chéo là vecto $\overrightarrow u ,\;\overrightarrow v$.

Ta dựng được hình hình hành ABCD và DEGH. Trong đó:  DC và DE nằm trên giá của vecto $\overrightarrow a$, DA và DH nằm trên giá của vecto $\overrightarrow b$, còn vecto $\overrightarrow u ,\;\overrightarrow v$ lần lượt là hai dường chéo.

Dễ thấy: $\overrightarrow u  = \overrightarrow {DA}  + \overrightarrow {DC} ,\;\overrightarrow v  = \overrightarrow {DH}  + \overrightarrow {DE}$

Mà $\overrightarrow {DA}  = 3\overrightarrow b ,\;\overrightarrow {DC}  = \overrightarrow a \;,\;\overrightarrow {DH}  = 3\overrightarrow b ,\;\overrightarrow {DE}  =  - 2\overrightarrow a .$

$\Rightarrow \overrightarrow u  = 2\overrightarrow b  + \overrightarrow a ,\;\,\overrightarrow v  = 3\overrightarrow b  - 2\overrightarrow a$