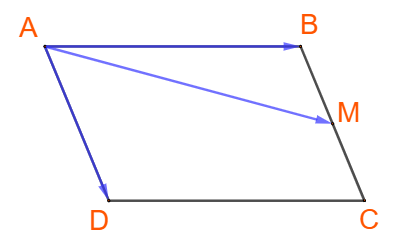
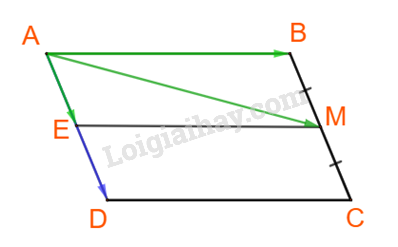
Giải bài 4.11 trang 58 SGK Toán 10 tập 1 – Kết nối tri thứcCho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Hãy biểu thị AM theo hai vecto AB và AD. Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Đề bài Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Hãy biểu thị \(\overrightarrow {AM} \) theo hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \). Phương pháp giải - Xem chi tiết Bước 1: Phân tích vecto \(\overrightarrow {AM} \) theo hai vecto cạnh. Bước 2: Biểu thị hai vecto cạnh theo vecto \(\overrightarrow {AB} \), \(\overrightarrow {AD} \). Lời giải chi tiết
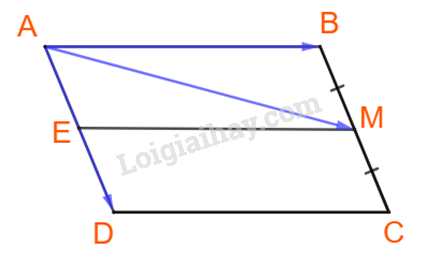
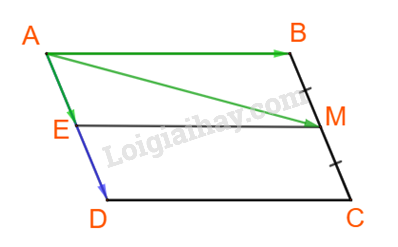
Từ M kẻ đường thẳng song song với AB, cắt AD tại E. Khi đó tứ giác ABME là hình bình hành. Do đó: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {AE} \). Dễ thấy: \(AE = BM = \frac{1}{2}BC = \frac{1}{2}AD\) \( \Rightarrow \overrightarrow {AE} = \frac{1}{2}\overrightarrow {AD} \) \( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \) Vậy \(\overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \) Chú ý khi giải +) Dựng hình hình hành sao cho đường chéo là vecto cần biểu thị, 2 cạnh của nó song song với giá của hai vecto đang biểu thị theo.
|