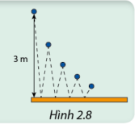
Giải mục 2 trang 54 SGK Toán 11 tập 1 - Cùng khám pháMột quả bóng được ném xuống từ độ cao 3 m. Độ cao mà quả bóng nảy lên bằng \(\frac{3}{5}\) độ cao trước đó (Hình 2.8).
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 2 Một quả bóng được ném xuống từ độ cao 3 m. Độ cao mà quả bóng nảy lên bằng \(\frac{3}{5}\) độ cao trước đó (Hình 2.8). Tính độ cao của lần nảy lên thứ nhất, thứ hai, thứ ba, thứ năm.
Phương pháp giải: - Dựa vào đầu bài, xác định \({u_1},q\). - Áp dụng công thức \({u_{n + 1}} = {u_n}.q\). Lời giải chi tiết: Độ cao mà quả bóng nảy lên bằng \(\frac{3}{5}\) độ cao trước đó nên ta lập được cấp số nhân với \(q = \frac{3}{5}\). Độ cao lần nảy thứ nhất là \(3.\frac{3}{5} = \frac{9}{5}\)\({u_1} = 3\) nên \({u_1} = \frac{9}{5}\). \( \Rightarrow {u_2} = \frac{9}{5}.\frac{3}{5} = \frac{{27}}{{25}};{u_3} = \frac{{27}}{{25}}.\frac{3}{5} = \frac{{81}}{{125}};{u_4} = \frac{{81}}{{125}}.\frac{3}{5} = \frac{{243}}{{625}};{u_5} = \frac{{243}}{{625}}.\frac{3}{5} = \frac{{729}}{{3125}}\) Vậy độ cao của lần thứ nhất là \(\frac{9}{5}\) m, lần thứ hai là \(\frac{{27}}{{25}}\) m, lần thứ ba là \(\frac{{81}}{{125}}\) m, lần thứ năm là \(\frac{{729}}{{3125}}\) m. Luyện tập 2 Một nước có dân số 25 triệu người vào đầu năm 2001. Nếu tỉ lệ tăng dân số hàng năm ổn định là 0,5%, tính dân số của nước đó vào đầu năm 2040. Phương pháp giải: Dựa vào đầu bài, xác định \({u_1},q,n\). Áp dụng công thức: \({u_n} = {u_1}.{q^{n - 1}}\left( {n \ge 2} \right)\). Lời giải chi tiết: Gọi \({u_1}\) là dân số năm 2001, \({u_2}\) là dân số năm 2002. \( \Rightarrow {u_1} = 25;{u_2} = 25 + 0,5\% .25 = 25,125\) \( \Rightarrow q = \frac{{{u_2}}}{{{u_1}}} = \frac{{25,125}}{{25}} = 1,005\) Tương tự như vậy với \({u_3},{u_4},...\) Ta sẽ lập được cấp số nhân với \({u_1} = 25,q = 1,005\). Vậy dân số của nước đó vào năm 2040 là: \({u_{39}} = {u_1}.{q^{38}} = 25.1,{005^{38}} \approx 30\) (triệu người).
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|