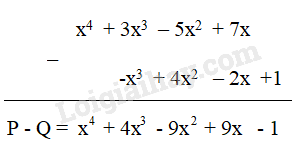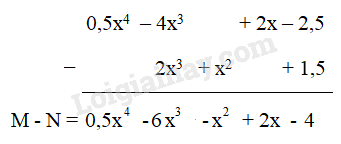Giải mục 2 trang 32, 33 SGK Toán 7 tập 2 - Kết nối tri thứcCho hai đa thức P = x^4 + 3x^3 – 5x^2 + 7x và Q = -x^3 + 4x^2 – 2x +1 Tìm hiệu P – Q bằng cách bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn. Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên...
Lựa chọn câu để xem lời giải nhanh hơn
2. Trừ hai đa thức một biến HĐ 1 Cho hai đa thức P = x4 + 3x3 – 5x2 + 7x và Q = -x3 + 4x2 – 2x +1 Tìm hiệu P – Q bằng cách bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn. Phương pháp giải: + Bước 1: Bỏ dấu ngoặc: Trước dấu ngoặc là dấu “ –“ thì ta bỏ dấu ngoặc đồng thời đổi dấu tất cả các số hạng trong ngoặc. +Bước 2: Nhóm các hạng tử cùng bậc + Bước 3: Thu gọn Lời giải chi tiết: Ta có: P – Q = x4 + 3x3 – 5x2 + 7x – (-x3 + 4x2 – 2x +1) = x4 + 3x3 – 5x2 + 7x + x3 - 4x2 + 2x – 1 = x4 + (3x3+ x3 ) + (– 5x2 - 4x2 ) + (7x + 2x ) – 1 = x4 + 4x3 – 9x2 + 9x – 1 HĐ 2 Cho hai đa thức P = x4 + 3x3 – 5x2 + 7x và Q = -x3 + 4x2 – 2x +1 Tìm hiệu P – Q bằng cách đặt tính trừ: đặt đa thức Q dưới đa thức P sao cho các hạng tử cùng bậc thẳng cột với nhau rồi trừ theo từng cột. Phương pháp giải: Bước 1: Đặt đa thức Q dưới đa thức P sao cho các hạng tử cùng bậc thẳng cột với nhau Bước 2: Trừ theo từng cột Lời giải chi tiết: LT 2 Cho hai đa thức: M = 0,5x4 – 4x3 + 2x – 2,5 và N = 2x3 + x2 + 1,5 Hãy tính hiệu M - N ( trình bày theo 2 cách) Phương pháp giải: Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc. Cách 2: Đặt tính trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi trừ theo từng cột. Lời giải chi tiết: Cách 1: M - N = (0,5x4 – 4x3 + 2x – 2,5) - ( 2x3 + x2 + 1,5) = 0,5x4 – 4x3 + 2x – 2,5 - 2x3 - x2 - 1,5 = 0,5x4 + (– 4x3 - 2x3 ) - x2 + 2x + (-2,5 - 1,5) = 0,5x4 + (– 6x3 ) - x2 + 2x + (-4) = 0,5x4 – 6x3 - x2 + 2x – 4 Cách 2: VD 2 Cho đa thức A = x4 – 3x2 – 2x + 1. Tìm các đa thức B và C sao cho: A + B = 2x5 + 5x3 – 2 A – C = x3 Phương pháp giải: B = (A + B) – A C = A – (A – C) Thực hiện phép trừ đa thức: Bỏ dấu ngoặc: Trước dấu ngoặc là dấu “ –“ thì ta bỏ dấu ngoặc đồng thời đổi dấu tất cả các số hạng trong ngoặc rồi nhóm các hạng tử cùng bậc Lời giải chi tiết: Ta có: B = (A + B) – A = 2x5 + 5x3 – 2 – (x4 – 3x2 – 2x + 1) = 2x5 + 5x3 – 2 – x4 + 3x2 + 2x - 1 = 2x5 – x4 + 5x3 + 3x2 + 2x + (-2 – 1) = 2x5 – x4 + 5x3 + 3x2 + 2x – 3 C = A – (A – C) = x4 – 3x2 – 2x + 1 – x3 = x4 – x3– 3x2 – 2x + 1 Vậy B = 2x5 – x4 + 5x3 + 3x2 + 2x – 3 C = x4 – x3– 3x2 – 2x + 1
|