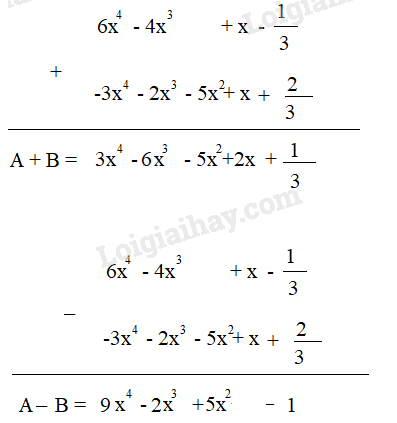Giải bài 7.14 trang 33 SGK Toán 7 tập 2 - Kết nối tri thứcCho hai đa thức: Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Cho hai đa thức: A=6x4−4x3+x−13;B=−3x4−2x3−5x2+x+23 Tính A + B và A - B Phương pháp giải - Xem chi tiết Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc. Cách 2: Đặt tính cộng (trừ) sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng (trừ ) theo từng cột. Lời giải chi tiết Cách 1: A+B=(6x4−4x3+x−13)+(−3x4−2x3−5x2+x+23)=6x4−4x3+x−13−3x4−2x3−5x2+x+23=(6x4−3x4)+(−4x3−2x3)−5x2+(x+x)+(−13+23)=3x4−6x3−5x2+2x+13A−B=(6x4−4x3+x−13)−(−3x4−2x3−5x2+x+23)=6x4−4x3+x−13+3x4+2x3+5x2−x−23=(6x4+3x4)+(−4x3+2x3)+5x2+(x−x)+(−13−23)=9x4−2x3+5x2−1A+B=(6x4−4x3+x−13)+(−3x4−2x3−5x2+x+23)=6x4−4x3+x−13−3x4−2x3−5x2+x+23=(6x4−3x4)+(−4x3−2x3)−5x2+(x+x)+(−13+23)=3x4−6x3−5x2+2x+13A−B=(6x4−4x3+x−13)−(−3x4−2x3−5x2+x+23)=6x4−4x3+x−13+3x4+2x3+5x2−x−23=(6x4+3x4)+(−4x3+2x3)+5x2+(x−x)+(−13−23)=9x4−2x3+5x2−1 Cách 2:
|