Giải mục 2 trang 32, 33, 34, 35 Chuyên đề học tập Toán 11 - Chân trời sáng tạoGọi M’ và N’ lần lượt là ảnh của M và N qua phép vị tự V(O, k). Từ các hệ thức: \(\overrightarrow {OM'} = k\overrightarrow {OM} ,\overrightarrow {ON'} = k\overrightarrow {ON} ,\overrightarrow {M'N'} = \overrightarrow {ON'} - \overrightarrow {OM'} \). Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh
Lựa chọn câu để xem lời giải nhanh hơn
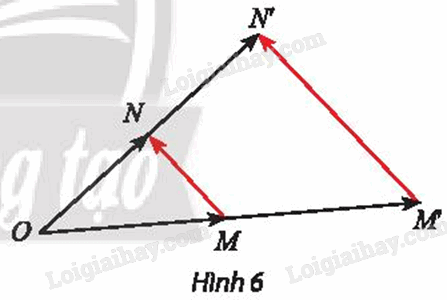
Khám phá 2 Gọi M’ và N’ lần lượt là ảnh của M và N qua phép vị tự V(O, k). Từ các hệ thức: \(\overrightarrow {OM'} = k\overrightarrow {OM} ,\overrightarrow {ON'} = k\overrightarrow {ON} ,\overrightarrow {M'N'} = \overrightarrow {ON'} - \overrightarrow {OM'} \). Biểu thị vectơ \(\overrightarrow {M'N'} \) theo vectơ \(\overrightarrow {MN} .\)
Phương pháp giải: Sử dụng quy tắc hiệu để biểu diễn Lời giải chi tiết: Ta có \(\overrightarrow {M'N'} = \overrightarrow {ON'} - \overrightarrow {OM'} \)′ \( = k\overrightarrow {ON} - k\overrightarrow {OM} = k\left( {\overrightarrow {ON} - \overrightarrow {OM} } \right) = k\overrightarrow {MN} \). Vậy \(\overrightarrow {M'N'} = k\overrightarrow {MN} \) Khám phá 3 Gọi A’, B’ và C’ lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép vị tự \({V_{(O,{\rm{ }}k)}}.\) Cho biết \(\overrightarrow {BA} = m\overrightarrow {BC} \) hai vectơ \(\overrightarrow {B'A'} \) và \(m\overrightarrow {B'C'} \) có bằng nhau không?
Phương pháp giải: Chứng minh hai vectơ \(\overrightarrow {B'A'} \) và \(m\overrightarrow {B'C'} \) cùng bằng vectơ thứ ba. Lời giải chi tiết: Theo bài, ta có A’, B’ lần lượt là ảnh của A, B qua \({V_{(O,{\rm{ }}k)}}.\) Áp dụng tính chất 1, ta được \(\overrightarrow {B'A'} = k\overrightarrow {BA} \) Chứng minh tương tự, ta được \(\overrightarrow {B'C'} = k\overrightarrow {BC} \) Ta có \(\overrightarrow {B'A'} = k\overrightarrow {BA} = k.m\overrightarrow {BC} = m.k\overrightarrow {BC} = m\overrightarrow {B'C'} \) Vậy hai vectơ \(\overrightarrow {B'A'} \) và \(m\overrightarrow {B'C'} \) bằng nhau. Thực hành 2 Cho tam giác ABC có G, H, O lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác. Gọi A’, B’, C’ lần lượt là trung điểm các cạnh BC, CA, AB. a) Tìm phép vị tự biến tam giác ABC thành tam giác A’B’C’. b) Chứng minh ba điểm H, G, O thẳng hàng. Phương pháp giải: Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự. Lời giải chi tiết:
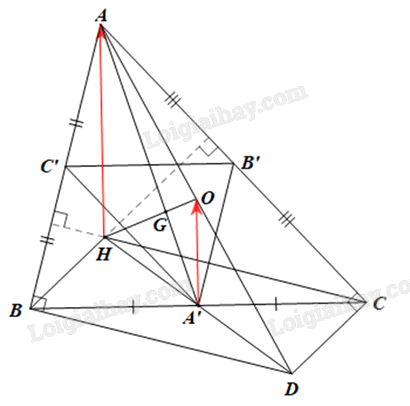
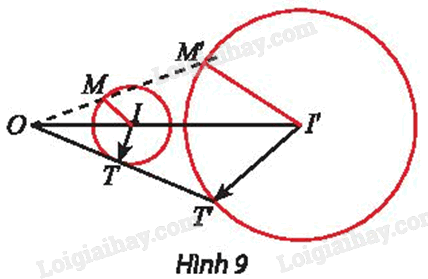
a) Để tìm phép vị tự biến ∆ABC thành ∆A’B’C’, ta tìm phép vị tự biến điểm A thành điểm A’, biến điểm B thành điểm B’, biến điểm C thành điểm C’. ∆ABC có A’ là trung điểm BC và G là trọng tâm. Theo tính chất trọng tâm của tam giác, ta có \(\overrightarrow {AG} = 2\overrightarrow {GA'} \) hay \(\overrightarrow {GA'} = - \frac{1}{2}\overrightarrow {GA} \) Suy ra A’ là ảnh của A qua \({V_{\left( {G, - \frac{1}{2}} \right)}}\) Chứng minh tương tự, ta được \({V_{\left( {G, - \frac{1}{2}} \right)}}\left( B \right) = B'\) và \({V_{\left( {G, - \frac{1}{2}} \right)}}\left( C \right) = C'\) Vậy \({V_{\left( {G, - \frac{1}{2}} \right)}}\) biến \(\Delta ABC\) thành b) Gọi AD là đường kính của đường tròn tâm O ngoại tiếp ∆ABC. Suy ra \(\widehat {ABD} = 90^\circ \) và O là trung điểm của AD. Do đó \(\;AB{\rm{ }} \bot {\rm{ }}BD.\) Mà \(CH \bot AB\) (do H là trực tâm của ∆ABC). Vì vậy BD // CH. Chứng minh tương tự, ta được BH // CD. Suy ra tứ giác BHCD là hình bình hành. Mà A’ là trung điểm BC (giả thiết). Do đó A’ cũng là trung điểm của DH. ∆ADH có A’O là đường trung bình của tam giác nên \(A'O = \frac{1}{2}HA\) và Suy ra \(\overrightarrow {A'O} = \frac{1}{2}\overrightarrow {HA} = - \frac{1}{2}\overrightarrow {AH} \) Ta có \(\overrightarrow {GO} = \overrightarrow {GA'} + \overrightarrow {A'O} = - \frac{1}{2}\overrightarrow {GA} - \frac{1}{2}\overrightarrow {AH} \) \( = - \frac{1}{2}\left( {\overrightarrow {GA} + \overrightarrow {AH} } \right) = - \frac{1}{2}\overrightarrow {GH} \) Khi đó \(\overrightarrow {GO} \) và \(\overrightarrow {GH} \) cùng phương nên ba điểm G, H, O thẳng hàng. Vậy ba điểm G, H, O thẳng hàng. Khám phá 4 Cho phép vị tự \({V_{\left( {O,{\rm{ }}k} \right)}}\) và đường tròn (C) tâm I bán kính r. Xét điểm M thuộc (C), gọi I’ và M’ là ảnh của I và M qua phép vị tự \({V_{\left( {O,{\rm{ }}k} \right)}}.\) a) Tính I’M’ theo r và k. b) Khi cho điểm M chạy trên đường tròn (C) thì M’ chạy trên đường nào?
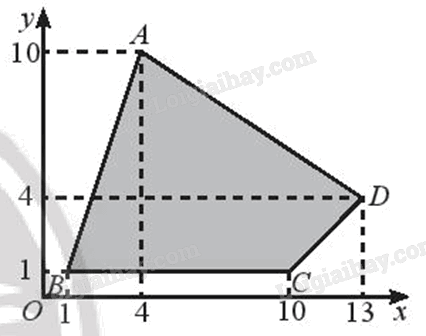
Phương pháp giải: Phép vị tự tỉ số k biến đoạn thẳng thành đoạn thẳng nhân lên với |k|, biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng |k|, biến đường tròn bán kính r thành đường tròn bán kính \(r' = |k|.r\). Lời giải chi tiết: a) Ta có \({V_{\left( {O,{\rm{ }}k} \right)}}\left( I \right){\rm{ }} = {\rm{ }}I'\) và \({V_{\left( {O,{\rm{ }}k} \right)}}\left( M \right){\rm{ }} = {\rm{ }}M'.\) Suy ra \(I'M'{\rm{ }} = {\rm{ }}\left| k \right|.IM{\rm{ }} = {\rm{ }}\left| k \right|.r.\) Vậy b) Theo đề, ta có \({V_{\left( {O,{\rm{ }}k} \right)}}\;\) biến điểm M thành điểm M’. Vậy khi M chạy trên đường tròn (C) thì M’ chạy trên đường tròn (C’) có tâm I’, bán kính \(r'{\rm{ }} = {\rm{ }}\left| k \right|.r\) là ảnh của (C) qua \({V_{\left( {O,{\rm{ }}k} \right)}}.\) Vận dụng 2 Vẽ Hình 11 ra giấy kẻ ô li và tìm ảnh của tứ giác ABCD qua phép vị tự \({V_{\left( {O, - \frac{1}{2}} \right)}}\).
Phương pháp giải: Để tìm ảnh của tứ giác ABCD qua phép vị tự \({V_{\left( {O, - \frac{1}{2}} \right)}}\) ta tìm ảnh của từng điểm A, B, C, D qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\). Sau đó nối chúng lại với nhau. Lời giải chi tiết:
Để tìm ảnh của tứ giác ABCD qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\), ta tìm ảnh của các điểm A, B, C, D qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\). Quan sát hình vẽ, ta thấy \(\;A\left( {4;{\rm{ }}10} \right),{\rm{ }}B\left( {1;{\rm{ }}1} \right),{\rm{ }}C\left( {10;{\rm{ }}1} \right),{\rm{ }}D\left( {13;{\rm{ }}4} \right).\) ⦁ Đặt là ảnh của A qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\) Suy ra \(\overrightarrow {O{A'}} = - \frac{1}{2}\overrightarrow {OA} \) với \(\overrightarrow {OA} = \left( {4;10} \right)\) và \(\overrightarrow {O{A'}} = \left( {{x_{A'}};{y_{A'}}} \right)\) Do đó \(\left\{ \begin{array}{l}{x_{A'}} = - \frac{1}{2}.4 = - 2\\{y_{A'}} = - \frac{1}{2}.10 = - 5\end{array} \right.\) Vì vậy tọa độ ⦁ Đặt \(B'\left( {{x_{B'}};{y_{B'}}} \right)\) là ảnh của B qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\) Suy ra \(\overrightarrow {O{B'}} = - \frac{1}{2}\overrightarrow {OB} \) với \(\overrightarrow {OB} = \left( {1;1} \right)\) và \(\overrightarrow {O{B'}} = \left( {{x_{B'}};{y_{B'}}} \right)\) Do đó \(\left\{ \begin{array}{l}{x_{B'}} = - \frac{1}{2}.1 = - \frac{1}{2}\\{y_{B'}} = - \frac{1}{2}.1 = - \frac{1}{2}\end{array} \right.\) Vì vậy tọa độ \(B'\left( { - \frac{1}{2}; - \frac{1}{2}} \right)\) ⦁ Đặt \(C'\left( {{x_{C'}};{y_{C'}}} \right)\) là ảnh của C qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\) Suy ra \(\overrightarrow {OC'} = - \frac{1}{2}\overrightarrow {OC} \) với \(\overrightarrow {OC} = \left( {10;1} \right)\) và \(\overrightarrow {OC'} = \left( {{x_{C'}};{y_{C'}}} \right)\) Do đó \(\left\{ \begin{array}{l}{x_{C'}} = - \frac{1}{2}.10 = - 5\\{y_{C'}} = - \frac{1}{2}.1 = - \frac{1}{2}\end{array} \right.\) Vì vậy tọa độ \(C'\left( { - 5; - \frac{1}{2}} \right)\) ⦁ Đặt \(D' = \left( {{x_{D'}};{y_{D'}}} \right)\) là ảnh của D qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\) Suy ra \(\overrightarrow {OD'} = - \frac{1}{2}\overrightarrow {OD} \)với \(\overrightarrow {OD} = \left( {13;4} \right)\) và \(\overrightarrow {O{D'}} = \left( {{x_{D'}};{y_{D'}}} \right)\) Do đó \(\left\{ \begin{array}{l}{x_{D'}} = - \frac{1}{2}.13 = - \frac{{13}}{2}\\{y_{D'}} = - \frac{1}{2}.4 = - 2\end{array} \right.\) Vì vậy tọa độ \(D'\left( { - \frac{{13}}{2}; - 2} \right)\) Vậy ảnh của tứ giác ABCD qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\) là tứ giác A’B’C’D’ có tọa độ các đỉnh là \(A'\left( {-2;{\rm{ }}-5} \right),B'\left( { - \frac{1}{2}; - \frac{1}{2}} \right),C'\left( { - 5; - \frac{1}{2}} \right),D'\left( { - \frac{{13}}{2}; - 2} \right)\)
|