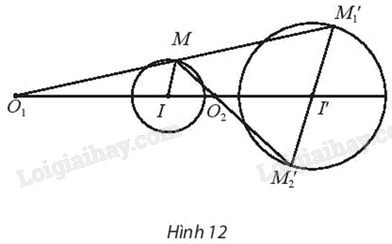
Giải bài 5 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạoCho hai đường tròn (I; R) và (I’; R’) (Hình 12) có tâm phân biệt và bán kính khác nhau. Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Cho hai đường tròn (I; R) và (I’; R’) (Hình 12) có tâm phân biệt và bán kính khác nhau. Hãy chứng minh có hai phép vị tự biến đường tròn (I; R) thành đường tròn (I’; R’).
Phương pháp giải - Xem chi tiết Quan sát hình 12, suy luận để chứng minh. Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự. Cần tìm được 2 giá trị của k thỏa mãn đề bài. Lời giải chi tiết Lấy điểm M bất kì thuộc \((I;{\rm{ }}R).\) Đường thẳng qua I’ và song song với IM cắt đường tròn (I’; R’) tại hai điểm và (giả sử M, nằm cùng phía đối với đường thẳng II’ và M, nằm khác phía đối với đường thẳng II’). Giả sử đường thẳng cắt đường thẳng II’ tại điểm O1 nằm ngoài đoạn OO’ và đường thẳng cắt đường thẳng II’ tại điểm O2 nằm trong đoạn II’. Ta có biến đường tròn (I; R) thành đường tròn (I’; R’). Suy ra \(R'{\rm{ }} = {\rm{ }}\left| k \right|.R.\) Do đó \(|k| = \frac{{R'}}{R}\) Mà \(k{\rm{ }} > {\rm{ }}0\) (do I, I’ nằm cùng phía đối với O1). Suy ra \(k = \frac{{R'}}{R}\) Ta có \({{\rm{V}}_{\left( {{{\rm{O}}_2},{\rm{k'}}} \right)}}\) biến đường tròn \(\left( {I;{\rm{ }}R} \right)\) thành đường tròn \(\left( {I';{\rm{ }}R'} \right).\) Chứng minh tương tự, ta được khi I, I’ nằm khác phía đối với O2, ta có \(k' = - \frac{{R'}}{R}\) Vậy ta có hai phép vị tự thỏa mãn yêu cầu bài toán là \({V_{\left( {{O_1},\frac{{R'}}{R}} \right)}}\) và \({V_{\left( {{O_2}, - \frac{{R'}}{R}} \right)}}\).
|