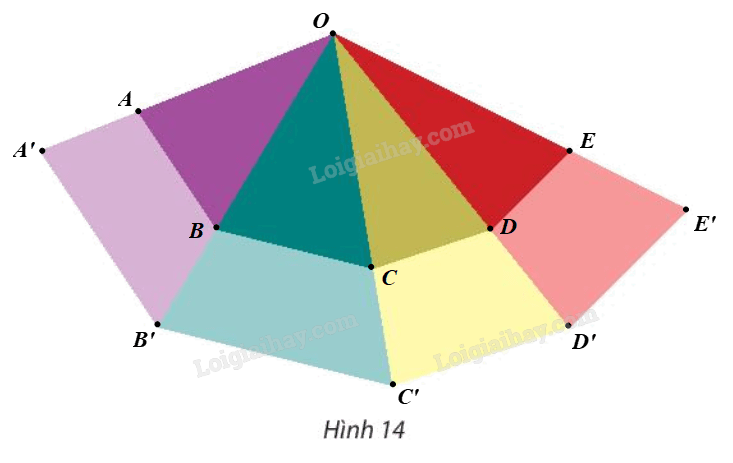
Giải bài 8 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Đề bài

Trong Hình 14, tìm phép vị tự được dùng để biến bốn tam giác nhỏ thành bốn tam giác lớn.

Lời giải chi tiết

Giả sử ta chọn điểm O như hình vẽ.

Ta đặt bốn tam giác nhỏ là $\Delta OAB,{\rm{ }}\Delta OBC,{\rm{ }}\Delta OCD\;$ và $\Delta$ODE và bốn tam giác lớn là OA’B’, $\Delta$OB’C’, $\Delta$OC’D’ và $\Delta$OD’E’ (hình vẽ).

Yêu cầu bài toán đưa về tìm phép vị tự biến $\Delta OAB,{\rm{ }}\Delta OBC,{\rm{ }}\Delta OCD\;$ và $\Delta$ODE lần lượt thành $\Delta$OA’B’, $\Delta$OB’C’, $\Delta$OC’D’ và $\Delta$OD’E’.

Tức là ta đi tìm phép vị tự biến các điểm O, A, B, C, D, E lần lượt thành O, A’, B’, C’, D’, E’.

Ta thấy O là giao điểm của các đường thẳng AA’, BB’, CC’, DD’, EE’.

Ta chứng minh các điểm O, A’, B’, C’, D’, E’ lần lượt là ảnh của các điểm O, A, B, C, D, E qua ${V_{\left( {O,{\rm{ }}k} \right)}}.$

Thật vậy, ta có ${V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right){\rm{ }} = {\rm{ }}A'.$

Suy ra $\overrightarrow {O{A'}}  = k\overrightarrow {OA}$ và $OA'{\rm{ }} = {\rm{ }}\left| k \right|.OA.$

Vì A, A’ nằm cùng phía đối với O nên $k{\rm{ }} > {\rm{ }}0$.

Do đó $k = \frac{{OA'}}{{OA}}$

Mà $k = \frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}}$ nên $\overrightarrow {OB'}  = k\overrightarrow {OB}$ do đó ${V_{\left( {O,{\rm{ }}k} \right)}}\left( B \right){\rm{ }} = {\rm{ }}B'.$

Tương tự như trên ta chứng minh được ${V_{\left( {O,{\rm{ }}k} \right)}}\left( C \right){\rm{ }} = {\rm{ }}C',{\rm{ }}{V_{\left( {O,{\rm{ }}k} \right)}}\left( D \right){\rm{ }} = {\rm{ }}D',{\rm{ }}{V_{\left( {O,{\rm{ }}k} \right)}}\left( E \right){\rm{ }} = {\rm{ }}E'.$

Vậy ${V_{\left( {O,\frac{{OA'}}{{OA}}} \right)}}$ là phép vị tự cần tìm.