Giải mục 1 trang 59, 60, 61 SGK Toán 8 - Cùng khám pháTa đã được học về tứ giác.
Lựa chọn câu để xem lời giải nhanh hơn
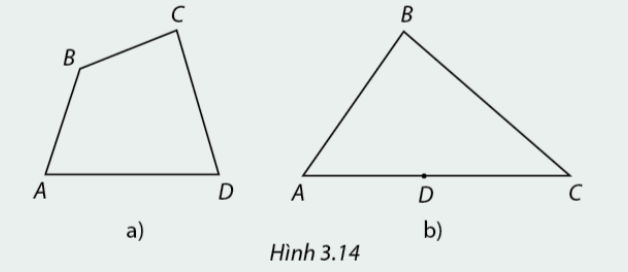
Hoạt động 1 Ta đã được học về tứ giác. Em hãy cho biết trong trường hợp nào của Hình 3.14, bốn đoạn thẳng AB, BC và AD tạo thành một tứ giác.
Phương pháp giải: Tứ giác \(ABCD\) là hình gồm bốn đoạn thẳng \(AB,BC,CD\) và \(DA\), trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng. Lời giải chi tiết: Hình a) có bốn đoạn thẳng \(AB,BC,CD\) và \(DA\) tạo thành một tứ giác, còn hình b) không phải hình tứ giác vì bốn đoạn thẳng \(AB,BC,CD\) và \(DA\) ở hình b) có \(AD,DC\) cùng nằm trên một đường thẳng. Hoạt động 2 Trong trường hợp nào ở Hình 3.16, tứ giác \(ABCD\) nằm về cùng một phía của từng đường thẳng trong các đường thẳng \(AB,BC,CD\) và \(DA\).
Phương pháp giải: Xét từng hình xem hình nào tứ giác \(ABCD\) nằm về cùng một phía của từng đường thẳng trong các đường thẳng \(AB,BC,CD\) và \(DA\). Lời giải chi tiết: Ta thấy hình a) có tứ giác \(ABCD\) nằm về cùng một phía của từng đường thẳng trong các đường thẳng \(AB,BC,CD\) và \(DA\). Còn hình b) và hình c) không có tứ giác \(ABCD\) nằm về cùng một phía của từng đường thẳng trong các đường thẳng \(AB,BC,CD\) và \(DA\). Luyện tập 1 Vẽ ba điểm A, B, C không thẳng hàng bất kì. Hãy vẽ thêm điểm D và E sao cho tứ giác ABCD lồi còn tứ giác ABCE không lồi. Phương pháp giải: Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của nó. Đầu tiên vẽ A, B, C không thẳng hàng bất kì, sau đó vẽ thêm điểm D và E sao cho tứ giác ABCD lồi còn tứ giác ABCE không lồi. Lời giải chi tiết: Tứ giác ABCD lồi Tứ giác ABCE không lồi Luyện tập 2 Viết tên tất cả các cặp cạnh kề nhau, cặp cạnh đối nhau, cặp đỉnh kề nhau, cặp đỉnh đối nhau còn lại của tứ giác \(ABCD\) trong Hình 3.17. Phương pháp giải: Hai đỉnh thuộc cùng một cạnh được gọi là hai đỉnh kề nhau, hai đỉnh không thuộc cùng một cạnh được gọi là hải đỉnh đối nhau. Đoạn thẳng nối hai đỉnh đối nhau gọi là đường chéo. Hai góc tại hai đỉnh đối nhau của tứ giác gọi là hai góc đối nhau. Hai cạnh có cùng đầu mút gọi là hai cạnh kề nhau, hai cạnh không có chung đầu mút gọi là hai cạnh đối nhau. Lời giải chi tiết: Cặp cạnh kề nhau: \(AB,AD\);\(DA,DC\);\(CD,CB\);\(BA,BC\). Cặp cạnh đối nhau: \(AB,DC;AB,BC\). Cặp đỉnh kề nhau: \(A,C;B,D;C,A\).
|