Giải mục 1 trang 30, 31, 32 Chuyên đề học tập Toán 11 - Chân trời sáng tạoTrong Hình 1, cho biết A’, B’, C’ lần lượt là trung điểm của OA, OB, OC. Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh
Lựa chọn câu để xem lời giải nhanh hơn
Khám phá 1 Trong Hình 1, cho biết A’, B’, C’ lần lượt là trung điểm của OA, OB, OC. a) Xét xem hai tam giác ABC và A’B’C’ đồng dạng không? b) Thảo luận nhóm để tìm xem có phép biến hình nào biến tam giác ABC thành tam giác A’B’C’ không?
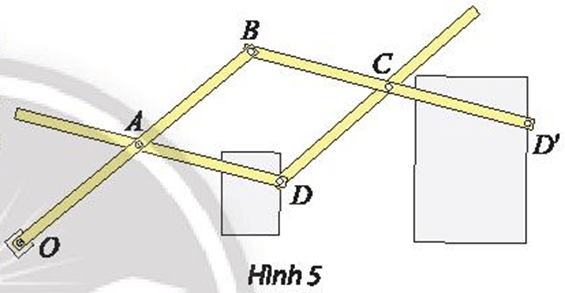
Phương pháp giải: Quan sát hình 1 và chứng minh 2 tam giác đồng dạng theo trường hợp c.c.c Lời giải chi tiết: a) Ta có A’ là trung điểm của OA. Suy ra OA′=12OA hay OA′OA=12 Chứng minh tương tự, ta được OB′OB=12 và OC′OC=12 Do OA′OA=OB′OB(=12) nên áp dụng định lí Thales đảo, ta được A’B’ // AB. Từ A’B’ // AB, theo hệ quả định lí Thales ta có: A′B′AB=OA′OA=12 hay ABA′B′=2 Chứng minh tương tự, ta được BCB′C′=2 và ACA′C′=2 Xét ΔABC và có: ABA′B′=BCB′C′=ACA′C′(=2) Vậy ΔABC đồng dạng với ΔA′B′C′ (c.c.c). b) Để tìm phép biến hình biến ∆ABC thành ∆A’B’C’, ta tìm phép biến hình biến điểm A thành điểm A’, biến điểm B thành điểm B’, biến điểm C thành điểm C’. Ta có A’ là trung điểm OA (giả thiết). Suy ra →OA′=12→OA Do đó phép biến hình biến điểm A thành điểm A’ thỏa mãn →OA′=12→OA(1) Thực hiện tương tự, ta được →OB′=12→OB Suy ra phép biến hình biến điểm B thành điểm B’ thỏa mãn →OB′=12→OB(2) Thực hiện tương tự, ta được →OC′=12→OC Do đó phép biến hình biến điểm C thành điểm C’ sao cho →OC′=12→OC(3) Từ (1), (2), (3), ta thu được phép biến hình biến ΔABC thành là phép biến hình biến ba điểm A, B, C thành ba điểm A’, B’, C’ thỏa mãn →OA′=12→OA,→OB′=12→OB,→OC′=12→OC với O là giao điểm của ba đường thẳng AA’, BB’, CC’. Thực hành 1 Trong mặt phẳng tọa độ Oxy, cho điểm M(3; 9). Tìm tọa độ các điểm M1 và M2 lần lượt là ảnh của M qua các phép vị tự V(O,3) và V(O,−2). Phương pháp giải: Nếu V(I,k)[M(x,y)]=M′(x′,y′). Khi đó, {x′−a=k(x−a)y′−b=k(y−b) với I(a;b) Lời giải chi tiết: Ta có →OM=(3;9) ⦁ Gọi M1(x1;y1), ta có →OM1=(x1;y1) Theo đề, ta có V(O,3)(M)=M1. Suy ra →OM1=3→OM Do đó {x1=3.3=9y1=3.9=27 Vì vậy tọa độ M1(9; 27). ⦁ Gọi M2(x2;y2), ta có →OM2=(x2;y2) Theo đề, ta có V(O,−2)(M)=M2. Suy ra →OM2=−2→OM Do đó {x2=−2.3=−6y2=−2.9=−18 Vì vậy tọa độ M2(−6;−18). Vậy M1(9;27),M2(−6;−18). Vận dụng 1 Thước vẽ truyền là một dụng cụ gồm bốn thanh gỗ hoặc kim loại được ghép với nhau nhờ bốn khớp xoay tại các điểm A, B, C, D sao cho ABCD là hình bình hành và ba điểm O, D, D’ thẳng hàng. Khi sử dụng, người vẽ ghim cố định điểm O xuống mặt giấy (thước vẫn có thể xoay quanh O). Đặt hai cây bút tại hai điểm D và D’. Khi đầu bút D vẽ hình ℋ, đầu bút D’ sẽ tự động vẽ truyền cho ta hình ℋ ’ là ảnh của ℋ.
a) Xác định tâm và tỉ số k của phép vị tự được sử dụng trong cây thước vẽ truyền ở Hình 5.
b) Nếu ngược lại cho đầu bút D’ vẽ hình ℋ ’ khi đó đầu bút D sẽ tự động vẽ truyền cho ta hình ℋ là ảnh của ℋ ’. Xác định phép vị tự trong trường hợp này. Phương pháp giải: Cho điểm O cố định và một số thực k, k≠0. Phép biến hình biến mỗi điểm M thành điểm M’ sao cho →OM′=k→OM được gọi là phép vị tự tâm O tỉ số k, kí hiệu V(O,k). O được gọi là tâm vị tự, k gọi là tỉ số vị tự. Lời giải chi tiết: a) Do ba điểm O, D, D’ thẳng hàng (giả thiết), suy ra →OD′=k→OD Do đó V(O,k)(D)=D′ và OD′=|k|.OD. Vì D, D’ nằm cùng phía đối với O nên k>0. Suy ra k=OD′OD Ta có AB // BD’ (do ABCD là hình bình hành) và ba điểm O, D, D’ thẳng hàng (giả thiết). Khi đó áp dụng định lí Thales, ta được k=ODOD′=OAOB Vậy phép vị tự cần tìm là V(O,OAOB) b) Từ câu a, ta có →OD′=k→OD(k>0). Suy ra →OD=1k→OD′ Khi đó V(O,1k)(D′)=D Ta có 1k=1:OAOB=OBOA Vậy phép vị tự cần tìm là V(O,OBOA)
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|