Giải đề thi học kì 1 toán lớp 8 năm 2019 - 2020 PGD Thanh Trì

Câu 1 (2 điểm):  Chọn chữ cái trước đáp án đúng

1. Kết quả của phép tính \(\left( {{a^2} + 3a + 9} \right)\left( {a - 3} \right)\) là:

A. \({a^3} - 27\)                     B. \({\left( {a - 3} \right)^3}\)

C. \({a^3} + 27\)                    D. \({\left( {a + 3} \right)^3}\)

2. Biểu thức \(\dfrac{{3x + 9}}{{6x - 3}}.\dfrac{{1 - 2x}}{{x + 3}}\) có kết quả rút gọn là:

A. \(1\)               B. \( - 1\)             C. \(3\)            D. \( - 3\)

3. Với \(x = 5\) thì đa thức \(10x - 25 - {x^2}\) có giá trị bằng:

A. \( - 100\)                      B. \(0\)

C. \(100\)                          D. Một giá trị khác

4. Phép chia \(5{x^{n - 1}}{y^4}:\left( {2{x^3}{y^n}} \right)\) là phép chia hết khi:

A. \(n > 4\)                        B. \(n \ge 4\)

C. \(n = 4\)                        D. \(n < 4\)

5. Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 3cm,\,\,BC = 5cm\). Tính diện tích tam giác \(ABC\).

A. \(6c{m^2}\)                        B. \(20c{m^2}\)

C. \(15c{m^2}\)                      D. \(12c{m^2}\)

6. Tam giác \(ABC\) có \(M,\,\,N\) lần lượt là trung điểm của \(AB,\,\,AC\), biết \(MN = 10cm\), độ dài cạnh \(BC\) bằng:

A. \(5cm\)                               B. \(10cm\)

C. \(15cm\)                             D. \(20cm\)

7. Hình nào sau đây chưa chắc có trục đối xứng?

A. Tam giác đều                     B. Hình chữ nhật

C. Hình thang                        D. Hình tròn

8. Tứ giác có các đỉnh là trung điểm các cạnh của một tứ giác có hai đường chéo vuông góc là:

A. Hình thang cân                   B. Hình chữ nhật

C. Hình thoi                           D. Hình vuông

Câu 2 (1,0 điểm) Tính hợp lí giá trị của biểu thức:

\(a)\,\,{75^2} + 150.25 + {25^2}\)                                                                             \(b)\,\,{2019^2} - 2019.19 - {19^2} - 19.1981\)

Câu 3 (1,0 điểm) Tìm \(x\) biết:

\(a)\,\,5x\left( {3 - x} \right) + x\left( {5 + 5x} \right) = 40\)                                   \(b)\,\,{\left( {x - 3} \right)^2} - x + 3 = 0\)

Câu 4 (1,0 điểm) Cho biểu thức \(A = \dfrac{{2x}}{{x + 3}} + \dfrac{2}{{x - 3}} + \dfrac{{{x^2} - x + 6}}{{9 - {x^2}}}\) với \(x \ne  \pm 3\).

a) Rút gọn biểu thức \(A\).

b) Tìm giá trị \(x\) nguyên để \(A\) nhận giá trị nguyên.

Câu 5 (1,0 điểm)  Cho hình thang vuông \(ABCD\), \(A = D = 90^\circ \)có \(CD = 2AB = 2AD\). Kẻ \(BH\) vuông góc với \(CD\).

a) Chứng minh rằng tứ giác \(ABHD\) là hình vuông.

b) Gọi \(M\) là trung điểm của \(BH\). Chứng minh \(A\) đối xứng với \(C\) qua \(M\).

c) Kẻ \(DI\) vuông góc với \(AC,\) \(DI,DM\) cắt \(AH\) lần lượt tại \(P\) và \(Q\). Chứng minh \(\Delta ADP = \Delta HDQ\).

d) Tứ giác \(BPDQ\) là hình gì?

Câu 6 (1,0 điểm) Cho \(\dfrac{x}{{y + z}} + \dfrac{y}{{z + x}} + \dfrac{z}{{x + y}} = 1\). Chứng minh \(\dfrac{{{x^2}}}{{y + z}} + \dfrac{{{y^2}}}{{z + x}} + \dfrac{{{z^2}}}{{x + y}} = 0\) 

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn HocTot.Nam.Name.Vn

Câu 1(TH):

1.

Phương pháp

Sử dụng hằng đẳng thức \({a^3} - {b^3} = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\).

Cách giải:

Ta có : \(\left( {{a^2} + 3a + 9} \right)\left( {a - 3} \right) = {a^3} - {3^3} = {a^3} - 27\)

Chọn A.

2.

Phương pháp

Phân tích tử thức và mẫu thức thành nhân tử rồi rút gọn.

Cách giải:

Ta có : \(\dfrac{{3x + 9}}{{6x - 3}}.\dfrac{{1 - 2x}}{{x + 3}}\)\( = \dfrac{{3\left( {x + 3} \right)}}{{3\left( {2x - 1} \right)}}.\dfrac{{ - \left( {2x - 1} \right)}}{{x + 3}} =  - 1\)

Chọn B.

3.

Phương pháp

Thay \(x = 5\) vào biểu thức đã cho tính giá trị.

Cách giải:

Ta có : \(10x - 25 - {x^2}\)\( =  - \left( {{x^2} - 10x + 25} \right) =  - {\left( {x - 5} \right)^2}\)

Với \(x = 5 \Rightarrow  - {\left( {x - 5} \right)^2} =  - {\left( {5 - 5} \right)^2} = 0\)

Chọn B

4.

Phương pháp

Đa thức \(P\left( x \right)\) chia hết cho \(Q\left( x \right)\) nếu chúng có cùng phần biến và lũy thừa của từng biến trong \(P\left( x \right)\) không nhỏ hơn lũy thừa của biến tương ứng trong \(Q\left( x \right)\)

Cách giải:

Để \(5{x^{n - 1}}{y^4}:\left( {2{x^3}{y^n}} \right)\) là phép chia hết thì \(\left\{ \begin{array}{l}n - 1 \ge 3\\4 \ge n\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}n \ge 4\\n \le 4\end{array} \right. \Leftrightarrow n = 4\)

Chọn C.

5.

Phương pháp

Sử dụng Pytago tính được \(AC\) rồi suy ra diện tích.

Cách giải:

Sử dụng Pytago ta có:

\(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow {3^2} + A{C^2} = {5^2}\) \( \Leftrightarrow A{C^2} = 16 \Leftrightarrow AC = 4cm\)

\( \Rightarrow S = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.3.4 = 6c{m^2}\).

Chọn A.

6.

Phương pháp

Sử dụng tính chất đường trung bình \(MN = \dfrac{1}{2}BC\).

Cách giải:

\(MN\) là đường trung bình của tam giác \(ABC\)\( \Rightarrow BC = 2MN = 20cm\).

Chọn D.

7.

Phương pháp

Tìm các trục đối xứng của mỗi hình và nhận xét.

Cách giải:

Tam giác đều có \(3\) trục đối xứng là \(3\) đường cao.

Hình chữ nhật có hai trục đối xứng là hai đường trung bình.

Hình tròn có vô số trục đối xứng là đường thẳng đi qua tâm.

Hình thang không phải là hình thang cân thì không có trục đối xứng.

Chọn C.

8.

Phương pháp

Sử dụng tính chất đường trung bình và dấu hiệu nhận biết : Hình bình hành có một góc vuông là hình chữ nhật.

Cách giải:

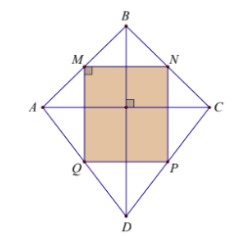
\(MN\) là đường trung bình của tam giác \(ABC\) nên \(MN//AC,MN = \dfrac{1}{2}AC\).

\(PQ\) là đường trung bình của tam giác \(ADC\) nên \(PQ//AC,PQ = \dfrac{1}{2}AC\).

\( \Rightarrow MN//PQ,MN = PQ\).

Do đó tứ giác \(MNPQ\) là hình bình hành.

Tam giác \(ABD\) có \(MQ\) là đường trung bình nên \(MQ//BD\).

Mà \(\left\{ \begin{array}{l}MN//AC\\MQ//BD\\AC \bot BD\end{array} \right.\)\( \Rightarrow MN \bot MQ\) \( \Rightarrow MNPQ\) là hình chữ nhật.

Chọn B.

Câu 2(VD):

Phương pháp

a) Sử dụng hằng đẳng thức \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\).

b) Nhóm các số hạng đưa về dạng tích.

Cách giải:

\(\begin{array}{l}a)\,\,{75^2} + 150.25 + {25^2}\\ = {75^2} + 2.75.25 + {25^2}\\ = {\left( {75 + 25} \right)^2}\\ = {100^2} = 10000\end{array}\)

\(\begin{array}{l}b)\,\,{2019^2} - 2019.19 - {19^2} - 19.1981\\ = \left( {{{2019}^2} - 2019.19} \right) - \left( {{{19}^2} + 19.1981} \right)\\ = 2019\left( {2019 - 19} \right) - 19\left( {19 + 1981} \right)\\ = 2019.2000 - 19.2000\\ = 2000.\left( {2019 - 19} \right)\\ = 2000.2000\\ = 4000000\end{array}\)

Câu 3(VD):

Phương pháp

a) Biến đổi đưa về dạng tích và giải phương trình.

b) Biến đổi đưa về dạng tích và giải phương trình tích \(AB = 0 \Leftrightarrow \left[ \begin{array}{l}A = 0\\B = 0\end{array} \right.\).

Cách giải:

\(\begin{array}{l}a)\,\,5x\left( {3 - x} \right) + x\left( {5 + 5x} \right) = 40\\ \Leftrightarrow 5x\left( {3 - x} \right) + 5x\left( {1 + x} \right) = 40\\ \Leftrightarrow 5x\left( {3 - x + 1 + x} \right) = 40\\ \Leftrightarrow 5x.4 = 40\\ \Leftrightarrow 20x = 40\\ \Leftrightarrow x = 40:20\\ \Leftrightarrow x = 2\end{array}\)

Vậy \(x = 2\).

\(\begin{array}{l}b)\,\,{\left( {x - 3} \right)^2} - x + 3 = 0\\ \Leftrightarrow {\left( {x - 3} \right)^2} - \left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {x - 3 - 1} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {x - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 4\end{array} \right.\end{array}\)

Vậy \(x \in \left\{ {3;4} \right\}\).

Câu 4(VD):

Phương pháp

a) Qui đồng, khử mẫu và rút gọn.

b) Sử dụng kiến thức về ước, bội để nhận xét giá trị nguyên.

Cách giải:

a) Rút gọn biểu thức \(A\).

Với \(x \ne  \pm 3\) ta có :

\(\begin{array}{l}A = \dfrac{{2x}}{{x + 3}} + \dfrac{2}{{x - 3}} + \dfrac{{{x^2} - x + 6}}{{9 - {x^2}}}\\ = \dfrac{{2x}}{{x + 3}} + \dfrac{2}{{x - 3}} - \dfrac{{{x^2} - x + 6}}{{{x^2} - 9}}\\ = \dfrac{{2x\left( {x - 3} \right) + 2\left( {x + 3} \right) - {x^2} + x - 6}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\\ = \dfrac{{2{x^2} - 6x + 2x + 6 - {x^2} + x - 6}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\\ = \dfrac{{{x^2} - 3x}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} = \dfrac{{x\left( {x - 3} \right)}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\\ = \dfrac{x}{{x + 3}}\end{array}\)

Vậy \(A = \dfrac{x}{{x + 3}}\).

b) Tìm giá trị \(x\) nguyên để \(A\) nhận giá trị nguyên.

Ta có:  \(A = \dfrac{x}{{x + 3}} = \dfrac{{x + 3 - 3}}{{x + 3}} = 1 - \dfrac{3}{{x + 3}}\)

Để \(A\) nhận giá trị nguyên thì \(x + 3 \in U\left( 3 \right) = \left\{ { \pm 1\,;\,\, \pm 3} \right\}\)

\(\begin{array}{l} \Rightarrow x + 3 = 1 \Rightarrow x =  - 2\,\,\left( {tm} \right)\\\,\,\,\,\,\,\,x + 3 =  - 1 \Rightarrow x = \, - 4\,\left( {tm} \right)\\\,\,\,\,\,\,\,x + 3 = 3 \Rightarrow x = 0\,\,\left( {tm} \right)\\\,\,\,\,\,\,\,x + 3 =  - 3 \Rightarrow x =  - 6\,\,\left( {tm} \right)\end{array}\)

Vậy \(x \in \left\{ { - 6\,;\,\, - 4\,;\,\, - 2\,;\,\,0} \right\}\)

Câu 5(VD):

Phương pháp

a) Sử dụng dấu hiệu nhận biết hình vuông : Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

b) Chứng minh \(ABCH\) là hình bình hành suy ra \(M\) là trung điểm \(AC\).

c) Chứng minh hai tam giác bằng nhau theo trường hợp g-c-g.

d) Sử dụng dấu hiệu nhận biết : Hình bình hành có hai đường chéo vuông góc là hình thoi.

Cách giải:

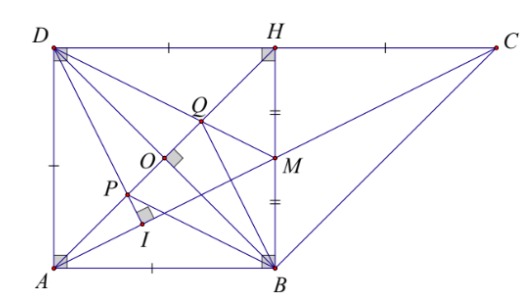
a) Chứng minh rằng tứ giác \(ABHD\) là hình vuông.

Ta có : \(\widehat {HDA} = \widehat {DAB} = \widehat {BHD} = 90^\circ \)\( \Rightarrow ABHD\) là hình chữ nhật.

Mà \(AB = AD\) \( \Rightarrow ABHD\) là hình vuông.

b) Gọi \(M\) là trung điểm của \(BH\). Chứng minh \(A\) đối xứng với \(C\) qua \(M\).

Ta có : \(\left\{ \begin{array}{l}AB//DH\\AB = DH\end{array} \right. \Rightarrow \left\{ \begin{array}{l}AB//HC\\AB = HC\end{array} \right.\)\( \Rightarrow ABCH\) là hình bình hành (dhnb)

Mà \(M\) là trung điểm của \(BH\) nên \(M\) là trung điểm của \(AC\) (t/c)

Suy ra \(A\) đối xứng với \(C\) qua \(M\).

c) Kẻ \(DI\) vuông góc với \(AC,\) \(DI,DM\) cắt \(AH\) lần lượt tại \(P\) và \(Q\). Chứng minh \(\Delta ADP = \Delta HDQ\).

Ta có : \(\widehat {PDA} = \widehat {MAB}\) (cùng phụ góc \(MAD\)) (1)

Xét \(\Delta MHD\) và \(\Delta MBA\) có :

\(\begin{array}{l}\widehat H = \widehat B = {90^0}\\MH = MB\left( {gt} \right)\\DH = AB\left( {hv} \right)\end{array}\)

\(\Delta MHD = \Delta MBA\left( {c - g - c} \right)\) \( \Rightarrow \widehat {MAB} = \widehat {MDH}\) (2)

Từ (1) và (2)\( \Rightarrow \widehat {PDA} = \widehat {MDH}\)

Xét \(\Delta ADP\) và \(\Delta HDQ\) có :

\(\widehat {QDH} = \widehat {PDA}\,\,\left( {cmt} \right)\)

\(\widehat {QHD} = \widehat {PAD} = 45^\circ \)

\(DH = DA\)

Vậy \(\Delta ADP = \Delta HDQ\,\,\,\left( {g.c.g} \right)\)

d) Tứ giác \(BPDQ\) là hình gì?

Gọi giao điểm của \(AH\) và \(DB\) là \(O\) \( \Rightarrow OB = OD\) (t/c) (3)

Ta có : \(\Delta ADP = \Delta HDQ\,\left( {cmt} \right)\)\( \Rightarrow AP = QH\) (cạnh t/ư)

Mà \(OA = OH \Rightarrow OQ = OP\) (4)

Xét tứ giác \(BPDQ\) có \(\left\{ \begin{array}{l}OP = OQ\\OD = OB\,\,\left( {cmt} \right)\\BD \bot PQ\end{array} \right.\) \( \Rightarrow BPDQ\) là hình thoi.

Câu 6(VDC): Cho \(\dfrac{x}{{y + z}} + \dfrac{y}{{z + x}} + \dfrac{z}{{x + y}} = 1\). Chứng minh \(\dfrac{{{x^2}}}{{y + z}} + \dfrac{{{y^2}}}{{z + x}} + \dfrac{{{z^2}}}{{x + y}} = 0\)

Phương pháp

Nhân cả hai vế của đẳng thức bài cho với \(x + y + z \ne 0\).

Cách giải:

Nhận xét: Nếu \(x + y + z = 0\) \( \Rightarrow \left\{ \begin{array}{l}x + y =  - z\\x + z =  - y\\y + z =  - x\end{array} \right.\) \( \Rightarrow \dfrac{x}{{y + z}} + \dfrac{y}{{z + x}} + \dfrac{z}{{x + y}} =  - 3\).

Suy ra \(x + y + z \ne 0\).

Ta có :

\(\dfrac{x}{{y + z}} + \dfrac{y}{{z + x}} + \dfrac{z}{{x + y}} = 1\)

\( \Leftrightarrow \left( {x + y + z} \right)\left( {\dfrac{x}{{y + z}} + \dfrac{y}{{z + x}} + \dfrac{z}{{x + y}}} \right)\)\( = x + y + z\)

\( \Leftrightarrow \dfrac{{{x^2}}}{{y + z}} + \dfrac{{xy}}{{z + x}} + \dfrac{{xz}}{{x + y}} + \dfrac{{xy}}{{y + z}}\)\( + \dfrac{{{y^2}}}{{z + x}} + \dfrac{{yz}}{{x + y}} + \dfrac{{xz}}{{y + z}} + \dfrac{{yz}}{{z + x}}\) \( + \dfrac{{{z^2}}}{{x + y}}\)\( = x + y + z\)

\( \Leftrightarrow \dfrac{{{x^2}}}{{y + z}} + \dfrac{{{y^2}}}{{z + x}} + \dfrac{{{z^2}}}{{x + y}}\)\( = \left( {x + y} \right)\dfrac{z}{{x + y}} + \left( {y + z} \right)\dfrac{x}{{y + z}} + \left( {z + x} \right)\dfrac{y}{{z + x}}\) \( = x + y + z\)

\( \Leftrightarrow \dfrac{{{x^2}}}{{y + z}} + \dfrac{{{y^2}}}{{z + x}} + \dfrac{{{z^2}}}{{x + y}} + x + y + z\)\( = x + y + z\)

\( \Leftrightarrow \dfrac{{{x^2}}}{{y + z}} + \dfrac{{{y^2}}}{{z + x}} + \dfrac{{{z^2}}}{{x + y}} = 0\)

HocTot.Nam.Name.Vn