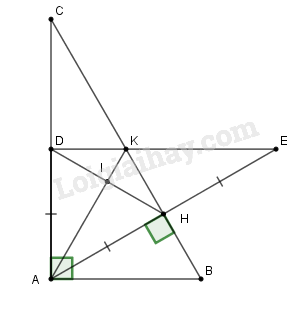
Đề thi học kì 1 môn toán lớp 7 năm 2019 - 2020 phòng GDĐT Thạch ThấtGiải chi tiết đề thi học kì 1 môn toán lớp năm 2019 - 2020 phòng GDĐT Thạch Thất với cách giải nhanh và chú ý quan trọng I. TRẮC NGHIỆM (2 điểm). Hãy khoanh tròn vào chữ cái đứng trước phương án trả lời đúng Câu 1 : Giá trị của hàm số \(y = f\left( x \right) = 3{x^2} + 2\) tại \(x = - 1\) bằng: A. \(2\) B. \(3\) C. \(4\) D. \(5\) Câu 2 : Cho \(\Delta ABC\) có góc \(A\) bằng \(70^\circ \), góc \(B\) bằng \(50^\circ \). Khi đó góc ngoài của \(\Delta ABC\) tại đỉnh \(C\) bằng: A. \(100^\circ \) B. \(110^\circ \) C. \(120^\circ \) D. \(130^\circ \) Câu 3 : Điểm nào sau đây thuộc đồ thị hàm số \(y = 4x\)? A. \(\left( {\dfrac{1}{3};\dfrac{4}{3}} \right)\) B. \(\left( {\dfrac{1}{3}; - \dfrac{4}{3}} \right)\) C. \(\left( { - \dfrac{4}{3}; - \dfrac{1}{3}} \right)\) D. \(\left( { - \dfrac{1}{3};\dfrac{4}{3}} \right)\) Câu 4 : Cho \(\Delta ABC\) có góc \(B\) bằng góc \(C\) và góc \(A\) bằng \(80^\circ \). Khi đó số đo của góc \(B\) bằng: A. \(40^\circ \) B. \(50^\circ \) C. \(60^\circ \) D. \(70^\circ \) II. TỰ LUẬN (8 điểm). Bài 1 (1,5 điểm). Thực hiện phép tính \(a)\,\,\dfrac{5}{6} + \dfrac{2}{3} - 0,5\) \(b)\,\,\left( - \dfrac{3}{4} + \dfrac{2}{3} \right): \dfrac{5}{11} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right):\dfrac{5}{{11}}\) \(c)\,\,{\left( { - 2} \right)^2} + \left| { - \dfrac{3}{2}} \right|.\sqrt {36} - \dfrac{8}{3}.\sqrt 9 \) Bài 2 (1,5 điểm). Tìm \(x,y\) biết: \(a)\,\,0,2 + \dfrac{2}{3}x = \dfrac{1}{3}\) \(b)\,\left| {2x - 1} \right| - \dfrac{1}{2} = \dfrac{1}{3}\) \(c)\,\,7x = 4y\) và \(x - y = - 21\) Bài 3 (1,5 điểm). Trong đợt thi đua chào mừng ngày Nhà giáo Việt Nam 20/11, số hoa điểm tốt của ba lớp 7A, 7B và 7C lần lượt tỉ lệ với các số \(12;\,\,10;\,\,9\). Biết rằng tổng số hoa điểm tốt của hai lớp 7B và 7C nhiều hơn lớp 7A là \(140\) bông. Hỏi mỗi lớp đạt được bao nhiêu bông hoa điểm tốt? Bài 4 (3,0 điểm). Cho tam giác \(ABC\) vuông tại \(A\) có góc \(B\) bằng \(60^\circ \). Vẽ \(AH\) vuông góc với \(BC\) tại \(H\). Trên cạnh \(AC\) lấy điểm \(D\) sao cho \(AD = AH.\) Gọi \(I\) là trung điểm của cạnh \(HD\). a) Chứng minh \(\Delta AHI = \Delta ADI\). Từ đó suy ra \(AI \bot HD\). b) Tia \(AI\) cắt cạnh \(HC\) tại điểm \(K\). Chứng minh \(\Delta AHK = \Delta ADK\) từ đó suy ra \(AB//KD.\) c) Trên tia đối của tia \(HA\) lấy điểm \(E\) sao cho \(HE = AH\). Chứng minh \(HB = HK\) và ba điểm \(D,K,E\) thẳng hàng. Bài 5 (0,5 điểm). Cho \(A = 1 - \dfrac{3}{4} + {\left( {\dfrac{3}{4}} \right)^2} - {\left( {\dfrac{3}{4}} \right)^3} \) \(+ {\left( {\dfrac{3}{4}} \right)^4} - ... - {\left( {\dfrac{3}{4}} \right)^{2017}} + {\left( {\dfrac{3}{4}} \right)^{2018}}\). Chứng tỏ \(A\) không phải là một số nguyên.
HƯỚNG DẪN GIẢI CHI TIẾT Thực hiện bởi ban chuyên môn HocTot.Nam.Name.Vn I. TRẮC NGHIỆM
Câu 1 (TH): Phương pháp Thay \(x = - 1\) vào hàm số đã cho rồi tính toán Cách giải: Thay \(x = - 1\) vào hàm số \(y = f\left( x \right) = 3{x^2} + 2\) ta được: \(f\left( { - 1} \right) = 3.{\left( { - 1} \right)^2} + 2 = 5\) Chọn D Câu 2 (TH): Phương pháp Tính góc ngoài tại đỉnh \(C\) bằng cách áp dụng: Góc ngoài tại một đỉnh của tam giác bằng tổng hai góc trong tại hai đỉnh không kề với đỉnh đó. Cách giải: Góc ngoài của \(\Delta ABC\) tại đỉnh \(C\) bằng: \(\widehat A + \widehat B = {70^0} + {50^0} = {120^0}.\) Chọn C Câu 3 (TH): Phương pháp Thay tọa độ các điểm vào hàm số đã cho để xác định điểm thuộc đồ thị Cách giải: Thay \(x = \dfrac{1}{3};y = \dfrac{4}{3}\) vào hàm số \(y = 4x\) ta được: \(\dfrac{4}{3} = 4.\dfrac{1}{3} \Leftrightarrow \dfrac{4}{3} = \dfrac{4}{3}\) (luôn đúng) Nên điểm có tọa độ \(\left( {\dfrac{1}{3};\dfrac{4}{3}} \right)\) thuộc đồ thị hàm số \(y = 4x.\) Chọn A Câu 4 (TH): Phương pháp Tổng ba góc trong tam giác bằng \({180^0}.\) Cách giải: Xét tam giác \(ABC\) có: \(\widehat A + \widehat B + \widehat C = {180^0}\) (tổng ba góc trong tam giác) Mà \(\widehat B = \widehat C \Rightarrow 2\widehat B + \widehat A = {180^0}\) \( \Rightarrow 2\widehat B = {180^0} - {80^0} \Rightarrow 2\widehat B = {100^0}\) \( \Rightarrow \widehat B = {50^0}.\) Chọn B II. TỰ LUẬN Bài 1(VD): Phương pháp Đưa về phân số rồi thực hiện tính toán theo thứ tự. Cách giải: \(a)\,\,\dfrac{5}{6} + \dfrac{2}{3} - 0,5\) \(\begin{array}{l} = \dfrac{5}{6} + \dfrac{2}{3} - \dfrac{1}{2}\\ = \dfrac{5}{6} + \dfrac{4}{6} - \dfrac{3}{6}\\ = \dfrac{{5 + 4 - 3}}{6}\\ = \dfrac{6}{6} = 1\end{array}\) \(b)\,\,\left( { - \dfrac{3}{4} + \dfrac{2}{3}} \right):\dfrac{5}{{11}} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right):\dfrac{5}{{11}}\) \(\begin{array}{l} = \left( { - \dfrac{3}{4} + \dfrac{2}{3}} \right).\dfrac{{11}}{5} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right).\dfrac{{11}}{5}\\ = \left( { - \dfrac{3}{4} + \dfrac{2}{3} - \dfrac{1}{4} + \dfrac{1}{3}} \right).\dfrac{{11}}{5}\\ = \left[ {\left( { - \dfrac{3}{4} - \dfrac{1}{4}} \right) + \left( {\dfrac{2}{3} + \dfrac{1}{3}} \right)} \right].\dfrac{{11}}{5}\\ = \left( { - 1 + 1} \right).\dfrac{{11}}{5}\\ = 0.\dfrac{{11}}{5}\\ = 0\end{array}\) \(c)\,\,{\left( { - 2} \right)^2} + \left| { - \dfrac{3}{2}} \right|.\sqrt {36} - \dfrac{8}{3}.\sqrt 9 \) \(\begin{array}{l} = 4 + \dfrac{3}{2}.6 - \dfrac{8}{3}.3\\ = 4 + 9 - 8\\ = 5\end{array}\) Bài 2(VD): Phương pháp a) Áp dụng qui tắc chuyển vế đổi dấu. b) Sử dụng \(\left| A \right| = B > 0\) thì \(A = B\) hoặc \(A = - B\). c) Sử dụng tính chất dãy tỉ số bằng nhau \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{{x - y}}{{a - b}}\) . Cách giải: \(a)\,\,0,2 + \dfrac{2}{3}x = \dfrac{1}{3}\) \(\begin{array}{l}\dfrac{2}{3}x = \dfrac{1}{3} - 0,2\\\dfrac{2}{3}x = \dfrac{1}{3} - \dfrac{1}{5}\\\dfrac{2}{3}x = \dfrac{2}{{15}}\\x = \dfrac{2}{{15}}:\dfrac{2}{3}\\x = \dfrac{1}{5}\end{array}\) \(b)\,\left| {2x - 1} \right| - \dfrac{1}{2} = \dfrac{1}{3}\) \(\begin{array}{l}\left| {2x - 1} \right| = \dfrac{1}{3} + \dfrac{1}{2}\\\left| {2x - 1} \right| = \dfrac{5}{6}\end{array}\) +) TH1: \(2x - 1 = \dfrac{5}{6}\) \(\begin{array}{l}2x = \dfrac{5}{6} + 1\\2x = \dfrac{{11}}{6}\\x = \dfrac{{11}}{6}:2\\x = \dfrac{{11}}{{12}}\end{array}\) +) TH2: \(2x - 1 = - \dfrac{5}{6}\) \(\begin{array}{l}2x = - \dfrac{5}{6} + 1\\2x = \dfrac{1}{6}\\x = \dfrac{1}{6}:2\\x = \dfrac{1}{{12}}\end{array}\) Vậy \(x = \dfrac{{11}}{{12}}\) hoặc \(x = \dfrac{1}{{12}}\). \(c)\,\,7x = 4y\) và \(x - y = - 21\) \(7x = 4y \Rightarrow \dfrac{x}{4} = \dfrac{y}{7}\) Áp dụng tính chất dãy tỉ số bằng nhau ta có: \(\dfrac{x}{4} = \dfrac{y}{7} = \dfrac{{x - y}}{{4 - 7}} = \dfrac{{ - 21}}{{ - 3}} = 7\) +) \(\dfrac{x}{4} = 7 \Rightarrow x = 7.4 = 28\). +) \(\dfrac{y}{7} = 7 \Rightarrow y = 7.7 = 49\). Vậy \(x = 28\) và \(y = 49\). Bài 3(VD): Phương pháp Gọi số điểm tốt của ba lớp \(7A,7B,7C\) lần lượt là \(x,y,z\). Lập mối quan hệ giữa \(x,y,z\) từ điều kiện bài toán và tìm \(x,y,z\) theo tính chất dãy tỉ số bằng nhau. Cách giải: Gọi số điểm tốt của ba lớp \(7A,7B,7C\) lần lượt là \(x,y,z\) (\(x,y,z \in {\mathbb{N}^*}\)) Vì số điểm tốt của ba lớp tỉ lệ với \(12,10,9\) nên \(\dfrac{x}{{12}} = \dfrac{y}{{10}} = \dfrac{z}{9}\) Vì tổng số điểm tốt của hai lớp 7B, 7C nhiều hơn lớp 7A là \(140\) nên \(y + z - x = 140\). Theo bài ra ta có : \(\dfrac{x}{{12}} = \dfrac{y}{{10}} = \dfrac{z}{9}\) và \(y + z - x = 140\). Áp dụng tính chất dãy tỉ số bằng nhau ta có : \(\dfrac{x}{{12}} = \dfrac{y}{{10}} = \dfrac{z}{9} = \dfrac{{y + z - x}}{{10 + 9 - 12}}\) \( = \dfrac{{140}}{7} = 20\) \( \Rightarrow \dfrac{x}{{12}} = 20 \Rightarrow x = 20.12 = 240\) \(\dfrac{y}{{10}} = 20 \Rightarrow y = 20.10 = 200\) \(\dfrac{z}{9} = 20 \Rightarrow z = 20.9 = 180\) Vậy số điểm tốt của các lớp 7A, 7B, 7C lần lượt là \(240,200,180\) điểm tốt. Bài 4 (VD): Phương pháp a) Sử dụng trường hợp bằng nhau cạnh cạnh cạnh của tam giác. b) Sử dụng trường hợp bằng nhau cạnh góc cạnh của tam giác và quan hệ từ vuông góc đến song song. c) Sử dụng các trường hợp bằng nhau của tam giác và tiên đề Ơ-clit về hai đường thẳng song song. Cách giải:
a) Chứng minh \(\Delta AHI = \Delta ADI\). Từ đó suy ra \(AI \bot HD\). Xét tam giác \(AHI\) và tam giác \(ADI\) có: +) \(AD = AH\left( {gt} \right)\) +) \(AI\) là cạnh chung +) \(ID = IH\) (vì \(I\) là trung điểm cạnh \(DH\)) Nên \(\Delta AHI = \Delta ADI\,\,\left( {c.c.c} \right)\) suy ra \(\widehat {AID} = \widehat {AIH}\) (hai góc tương ứng bằng nhau) Lại có \(\widehat {AID} + \widehat {AIH} = {180^0}\) (hai góc kề bù) nên \(\widehat {AID} = \widehat {AIH} = \dfrac{{{{180}^0}}}{2} = {90^0}\) Hay \(AI \bot DH\,\left( {dpcm} \right)\) Suy ra được \(AI \bot HD\). b) Tia \(AI\) cắt cạnh \(HC\) tại điểm \(K\). Chứng minh \(\Delta AHK = \Delta ADK\) từ đó suy ra \(AB//KD.\) Theo câu a) ta có: \(\Delta AHI = \Delta ADI\,\,\left( {c.c.c} \right)\) suy ra \(\widehat {DAI} = \widehat {IAH}\) (hai góc tương ứng bằng nhau) Xét tam giác \(ADK\) và tam giác \(AHK\) có: +) \(AD = AH\left( {gt} \right)\) +) \(\widehat {DAI} = \widehat {IAH}\) (cmt) +) \(AK\) là cạnh chung Nên \(\Delta ADK = \Delta AHK\,\,\left( {c.g.c} \right)\) suy ra \(\widehat {ADK} = \widehat {AHK} = {90^0}\) (do \(AH \bot AB\)) Suy ra \(DK \bot AC\) Lại có \(AB \bot AC\) (do \(\widehat A = {90^0}\)) Suy ra \(DK//AB\) (vì cùng vuông góc với \(AC\)) (đpcm) c) Trên tia đối của tia \(HA\) lấy điểm \(E\) sao cho \(HE = AH\). Chứng minh \(HB = HK\) và ba điểm \(D,K,E\) thẳng hàng. Tam giác \(AHB\) vuông tại \(H\) có \(\widehat {HBA} = {60^0}\left( {gt} \right)\) nên \(\widehat {HAB} = {180^0} - \widehat {AHB} - \widehat {HBA} \) \(= {180^0} - {90^0} - {60^0} = {30^0}\) Lại có \(\widehat {HAB} + \widehat {HAK} + \widehat {KAC} = {90^0}\) mà \(\widehat {HAK} = \widehat {DAK}\) (theo câu b) Suy ra \(\widehat {HAK} = \dfrac{{{{90}^0} - \widehat {HAB}}}{2} \) \(= \dfrac{{{{90}^0} - {{30}^0}}}{2} = {30^0}\) Do đó \(\widehat {HAK} = \widehat {HAB}\left( { = {{30}^0}} \right)\) Xét tam giác \(ABH\) và tam giác \(AKH\) có: +) \(\widehat {HAK} = \widehat {HAB}\left( {cmt} \right)\) +) \(AH\) cạnh chung +) \(\widehat {AHB} = \widehat {AHK} = {90^0}\,\,\left( {do\,\,AH \bot BC} \right)\) Nên \(\Delta ABH = \Delta AKH\,\left( {g - c - g} \right)\) suy ra \(HB = HK\) (hai cạnh tương ứng bằng nhau) Xét tam giác \(ABH\) và tam giác \(EKH\) có: +) \(HB = HK\,\left( {cmt} \right)\) +) \(\widehat {AHB} = \widehat {KHE}\) (hai góc đối đỉnh) +) \(AH = HE\,\left( {gt} \right)\) Nên \(\Delta ABH = \Delta EKH\,\left( {c - g - c} \right)\) suy ra \(\widehat {KEH} = \widehat {HAB}\) (hai góc tương ứng bằng nhau) Mà hai góc này ở vị trí so le trong nên \(KE//AB\) (*) Theo câu a) ta có \(DK//AB\) (**) Từ (*) và (**) suy ra \(D,K,E\) thẳng hàng. Bài 5(VDC): Phương pháp Nhân \(A\) với \(\dfrac{3}{4}\) rồi thực hiện cộng \(A\) với \(\dfrac{3}{4}A\). Thu gọn kết quả và suy ra \(A\). Cách giải: \(A = 1 - \dfrac{3}{4} + {\left( {\dfrac{3}{4}} \right)^2} - {\left( {\dfrac{3}{4}} \right)^3} + {\left( {\dfrac{3}{4}} \right)^4} \)\(- ... - {\left( {\dfrac{3}{4}} \right)^{2017}} + {\left( {\dfrac{3}{4}} \right)^{2018}}\) \( \Rightarrow \dfrac{3}{4}A = \dfrac{3}{4} - {\left( {\dfrac{3}{4}} \right)^2} + {\left( {\dfrac{3}{4}} \right)^3} \)\(- {\left( {\dfrac{3}{4}} \right)^4} + ... + {\left( {\dfrac{3}{4}} \right)^{2017}} \) \(- {\left( {\dfrac{3}{4}} \right)^{2018}} + {\left( {\dfrac{3}{4}} \right)^{2019}}\) \( \Rightarrow A + \dfrac{3}{4}A = 1 + {\left( {\dfrac{3}{4}} \right)^{2019}}\) \( \Rightarrow \dfrac{7}{4}A = 1 + {\left( {\dfrac{3}{4}} \right)^{2019}}\) \( \Rightarrow A = \left[ {1 + {{\left( {\dfrac{3}{4}} \right)}^{2019}}} \right].\dfrac{4}{7}\) Suy ra \(A > 0\,\,\,\,\,\,\,\left( 1 \right)\) Vì \({\left( {\dfrac{3}{4}} \right)^{2019}} < \dfrac{3}{4} \) \(\Rightarrow A < \left( {1 + \dfrac{3}{4}} \right).\dfrac{4}{7} = 1\,\,\,\,\,\,\,\left( 2 \right)\) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(0 < A < 1\). Vậy \(A\) không phải là số nguyên. Hết HocTot.Nam.Name.Vn
|