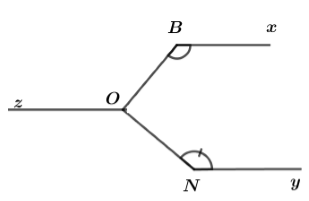
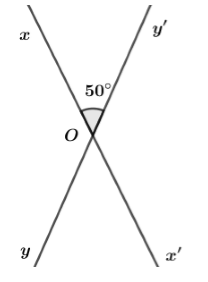
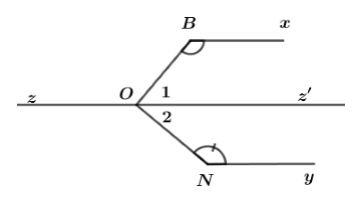
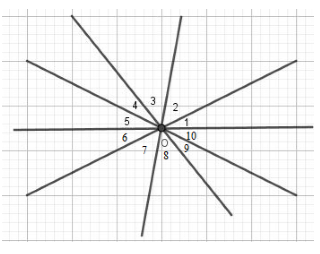
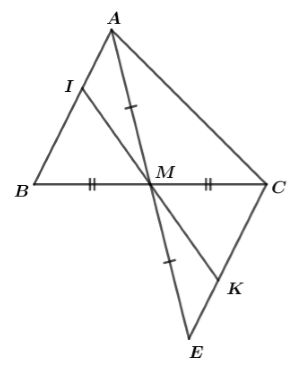
Đề thi học kì 1 môn toán lớp 7 năm 2019 - 2020 phòng GDĐT Bình XuyênGiải chi tiết đề thi học kì 1 môn toán lớp 7 năm 2019 - 2020 phòng GDĐT Bình Xuyên với cách giải nhanh và chú ý quan trọng PHẦN I: TRẮC NGHIỆM KHÁCH QUAN (3 điểm). Câu 1. Kết quả của phép tính −14−3−8 là bao nhiêu ? A. −58⋅ B. −18⋅ C. −13⋅ D. 18⋅ Câu 2. Giá trị của x thỏa mãn đẳng thức 2x=(22)3 là A. 5. B. 6. C. 26. D. 8. Câu 3. Giá trị của x thỏa mãn tỉ lệ thức x16=38 là A. 6. B. −6. C. 2. D. 3. Câu 4. Cho am=bn=2a−3b?⋅ Biểu thức cần điền vào dấu “ ? ” là biểu thức nào sau đây ? A. 2m+3n. B. 2m−3n. C. 2n+3m. D. 2n−3m. Câu 5. Viết số 5,(3) dưới dạng phân số tối giản, ta được kết quả là A. 53⋅ B. 83⋅ C. 163⋅ D. 5310⋅ Câu 6. Làm tròn số 2,345 đến chữ số thập phân thứ hai sau dấu phẩy ta được kết quả là bao nhiêu ? A. 2,34. B. 2,35. C. 2,30. D. 2,4. Câu 7. Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k (k là hằng số khác 0) nếu A. y=kx. B. y=kx⋅ C. y=xk⋅ D. y=1kx⋅ Câu 8. Công thức nào sau đây cho ta quan hệ tỉ lệ nghịch giữa x và y? A. 5y=3x. B. y=−2x. C. xy=2019 D. x+y=2020. Câu 9. Đường thẳng xx′ cắt đường thẳng yy′ tại O, biết ^xOy′=50∘, số đo góc x′Oy bằng bao nhiêu ? A. 140∘. B. 130∘. C. 40∘. D.50∘. Câu 10. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng sẽ A. song song với nhau B. vuông góc với nhau C. trùng nhau D. cắt nhau. Câu 11. Tổng các góc ngoài của một tam giác bằng bao nhiêu độ ? A. 90∘. B. 180∘. C. 360∘. D. 270∘. Câu 12. Cho ΔABC=ΔMNP và AC=5cm. Cạnh nào của tam giác MNP có độ dài bằng 5cm? A. PN. B. MN. C. PM. D. AM. PHẦN II: TỰ LUẬN (6 điểm). Câu 13: (1 điểm) Thực hiện phép tính a) A=−53⋅311+−1318⋅311 b) B=(−3)30.155257.(−9)2 Câu 14: (1,5 điểm) a) Lập tất cả các tỉ lệ thức từ đẳng thức 13.18=9.26. b) Cho tỉ lệ thức ab=cd, chứng minh rằng aa+b=cc+d⋅ c) Cho x,y,z thỏa mãn x3=y5=z6 và x−2y+3z=−33. Tìm giá trị của x,y,z. Câu 15: (0,5 điểm) Người ta chia số 520 thành 3 phần a,b,c tỉ lệ nghịch với 2,3,4. Tìm a,b,c. Câu 16: (1,5 điểm) a) Cho hình vẽ. Biết Bx//Oz,Oz//Ny và ^xBO=130∘,^ONy=140∘. Tính ^NOB. b) Cho 5 đường thẳng phân biệt sao cho không có 2 đường thẳng nào song song. Chứng minh tồn tại một cặp đường thẳng tạo với nhau một góc không quá 36∘. Câu 17: (2 điểm) Cho tam giác ABC, gọi M là trung điểm của BC. Trên tia AM lấy điểm E sao cho M là trung điểm của AE. a) Chứng minh AB=CE và AB//CE. b) Trên đoạn thẳng AB lấy điểm I và trên đoạn thẳng CE lấy điểm K sao cho AI=EK. Chứng minh rằng ba điểm I,M,K thẳng hàng. Câu 18: (0,5 điểm) Tìm hai số khác 0 biết rằng tổng, hiệu, tích của chúng tỉ lệ với 5,1,12. HẾT
HƯỚNG DẪN GIẢI CHI TIẾT Thực hiện: Ban chuyên môn HocTot.Nam.Name.Vn PHẦN I: TRẮC NGHIỆM
Câu 1 (NB): Phương pháp: - Viết phân số thứ hai thành phân số có mẫu số dương - Tìm mẫu số chung. - Thực hiện phép tính với tử, giữ nguyên mẫu chung rồi chọn đáp án đúng. Cách giải: −14−3−8=−14−−38=−2+38=18 Chọn D. Câu 2 (NB): Phương pháp: Vận dụng kiến thức (am)n=am.n để tìm giá trị của x. Cách giải: 2x=(22)32x=22.3=26x=6 Chọn B. Câu 3 (NB): Phương pháp: Áp dụng tính chất của tỉ lệ thức ab=cd thì ad=bc Cách giải: x16=38x.8=16.3x=16.38 x=6. Chọn A. Câu 4 (NB): Phương pháp: Áp dụng kiến thức về tính chất dãy tỉ số bằng nhau : ab=cd=a±cb±d Cách giải: Vì am=bn⇒2a2m=3b3n=2a−3b2m−3n Vậy ?=2m−3n. Chọn B. Câu 5 (NB): Phương pháp: Vận dụng kiến thức : 19=0,(1);199=0,(01);1999=0,(001) Cách giải: 5,(3)=5+3.0,(1)=5+3⋅19=5+13=163 Chọn C. Câu 6 (NB): Phương pháp: Áp dụng quy tắc làm tròn số: - Nếu chữ số đầu tiên bỏ đi nhỏ hơn 5 thì ta giữ nguyên bộ phận còn lại. - Nếu chữ số đầu tiên bỏ đi lớn hơn hoặc bằng 5 thì ta cộng thêm 1 đơn vị vào chữ số cuối cùng của bộ phận còn lại. Cách giải: Số 2,345 có chữ số cần bỏ đi bằng 5 nên khi làm tròn đến chữ số thập phân thứ hai sau dấu phẩy ta được số 2,35. Chọn B. Câu 7 (NB): Phương pháp: Nhẩm lại định nghĩa hai đại lượng tỉ lệ thuận đã học. Cách giải: Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k (k là hằng số khác 0) thì y=kx. Chọn A. Câu 8 (NB): Phương pháp: Nhẩm lại khái niệm hai đại lượng tỉ lệ nghịch đã học : Hai đại lượng tỉ lệ nghịch x và y liên hệ với nhau bởi công thức y=ax hay xy=a (với a là một số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a. Cách giải: Đáp án A. 5y=3x⇒y=3x5 hay đại lượng y tỉ lệ thuận với đại lượng x. Đáp án B. y và x là hai đại lượng tỉ lệ thuận với hệ số tỉ lệ là −2 . Đáp án C. y và x là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ là 2019. Đáp án D. y và x không tỉ lệ thuận cũng không tỉ lệ nghịch. Chọn C. Câu 9 (NB): Phương pháp: - Vẽ hình. - Vận dụng định lý : Hai góc đối đỉnh thì bằng nhau. Cách giải: Ta có : Ox là tia đối của Ox′; Oy là tia đối của Oy′ (do cách vẽ) Vậy ^xOy′ và ^x′Oy là hai góc đối đỉnh ⇒^xOy′=^x′Oy=50∘. Chọn D. Câu 10 (NB): Phương pháp: Áp dụng quan hệ giữa tính vuông góc và tính song song của ba đường thẳng. Cách giải: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau. Câu 11 (NB): Phương pháp: Áp dụng kiến thức : Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó. Cách giải: Giả sử có ΔABC Góc ngoài tại đỉnh A bằng ˆB+ˆC Góc ngoài tại đỉnh bằng ˆA+ˆC Góc ngoài tại đỉnh C bằng ˆB+ˆA Tổng ba góc ngoài của tam giác ABC bằng 2(ˆA+ˆB+ˆC) Mà ˆA+ˆB+ˆC=180∘ nên tổng ba góc ngoài của tam giác bằng 2.180∘=360∘. Chọn C. Câu 12 (NB): Phương pháp: Vận dụng tính chất : Hai tam giác bằng nhau thì có các cặp cạnh tương ứng bằng nhau. Cách giải: ΔABC=ΔMNP⇒AC=MP (cặp cạnh tương ứng) ⇒MP=5cm. Chọn C. PHẦN II. TỰ LUẬN Câu 13 (NB): Phương pháp: a) Áp dụng tính chất : a×b+a×c=a×(b+c) b) Sử dụng kiến thức : aman=am−n Cách giải: a) A=−59⋅311+−1318⋅311 A=(−59+−1318)⋅311A=−10+(−13)18⋅311A=−23.36.3.11A=−2366 b) B=(−3)30.155257.(−9)2 B=330.155257.92 B=330.35.55(52)7.(32)2B=335.55514.34B=33159 Câu 14 (NB): Phương pháp: a) Áp dụng kiến thức : Nếu ad=bc và a,b,c,d≠0 thì ab=cd;ac=bd;db=ca;dc=ba. b) Áp dụng tính chất : Nếu ab=cd thì ad=bc. c) Áp dụng tính chất dãy tỉ số bằng nhau và chứng minh. ab=cd=ef⇒ab=cd=ef=a+c+eb+d+f=a−c+eb−d+f Cách giải: a) Lập tất cả các tỉ lệ thức từ đẳng thức 13.18=9.26. Ta lập được các tỉ lệ thức sau : 139=2618;189=2613;1326=918;913=1826 b) Cho tỉ lệ thức ab=cd, chứng minh rằng aa+b=cc+d⋅ Ta có : ab=cd⇒ad=bc Cộng hai vế với ac ta được: ac+ad=ac+bc ⇔a(c+d)=c(a+b) hay aa+b=cc+d. c) Cho x,y,z thỏa mãn x3=y5=z6 và x−2y+3z=−33. Tìm giá trị của x,y,z. Ta có x3=y5=z6⇒x3=2y10=3z18 Mà x−2y+3z=−33 Áp dụng tính chất dãy tỉ số bằng nhau ta được : x3=2y10=3z18=x−2y+3z3−10+18=−3311=−3 ⇒{x3=−3⇒x=−3.3=−9y5=−3⇒y=−3.5=−15z6=−3⇒z=−3.6=−18 Vậy giá trị của x,y,z cần tìm lần lượt là −9,−15,−18. Câu 15 (NB): Phương pháp: Vận dụng kiến thức về hai đại lượng tỉ lệ nghịch và tính chất của dãy tỉ số bằng nhau, từ đó tìm lời giải cho bài toán. Cách giải: Giả sử ba phần a,b,c lần lượt tỉ lệ nghịch với 2,3,4 theo hệ số tỉ lệ k thì ta có : a.2=b.3=c.4=k Ta có : a.2=b.3⇒a3=b2⇒a6=b4 Và 3b=4c⇒b4=c3 ⇒a6=b4=c3 Mặt khác : a+b+c=520 Áp dụng tính chất dãy tỉ số bằng nhau ta được: a6=b4=c3=a+b+c13=52013=40 {a6=40⇒a=40.6=240b4=40⇒b=40.4=160c3=40⇒c=40.3=120 Vậy ba số a,b,c cần tìm lần lượt là 240,160,120. Câu 16 (NB): Phương pháp: a) Vận dụng kiến thức: Khi một đường thẳng cắt hai đường thẳng song song thì tạo thành các cặp góc so le trong bằng nhau, các cặp góc đồng vị bằng nhau hoặc các cặp góc trong cùng phía bù nhau. b) Lấy một điểm O bất kì trong mặt phẳng, qua O dựng các đường thẳng song song với các đường thẳng đã cho. Chứng minh bằng phản chứng, giả sử các góc tạo thành đều lớn hơn 360 suy ra điều mâu thuẫn và kết luận. Cách giải: a) Cho hình vẽ. Biết Bx//Oz,Oz//Ny và ^xBO=130∘,^ONy=140∘. Tính ^NOB. Ta có Bx//Oz;Oz//Ny nên Vẽ tia Oz′ là tia đối của tia Oz Ta có Oz′//Bx nên ^xBO+^O1=180∘ (hai góc trong cùng phía) Mà ^xBO=130∘ nên ^O1=180∘−130∘=50∘ Chứng minh tương tự ta có ^ONy+^O2=180∘ (do Oz′//Ny) Tia Oz′ chia góc NOB thành hai góc O1 và góc O2 nên ^NOB=^O1+^O2=50∘+40∘=90∘ b) Cho 5 đường thẳng phân biệt sao cho không có 2 đường thẳng nào song song. Chứng minh tồn tại một cặp đường thẳng tạo với nhau một góc không quá 36∘. Lấy một điểm O bất kì, qua O kẻ các đường thẳng song song với 5 đường thẳng đã cho. Khi đó tạo thành 10 góc tại O có tổng số đo bằng 3600, trong đó có 5 cặp góc đối đỉnh ^O1=^O6,^O2=^O7,^O3=^O8, ^O4=^O9,^O5=^O10 nên: ^O1+^O2+^O3+^O4+^O5=^O6+^O7+^O8+^O9+^O10=36002=1800 Giả sử không tồn tại cặp đường thẳng nào tạo với nhau một góc không quá 360 hay tất cả các góc tạo thành đều lớn hơn . Khi đó ^O1>360,^O2>360,^O3>360,^O4>360,^O5>360 ⇒^O1+^O2+^O3+^O4+^O5>360+360+360+360+360=1800 (mâu thuẫn vì ^O1+^O2+^O3+^O4+^O5=1800) Vậy phải tồn tại một cặp đường thẳng tạo với nhau một góc không quá 360. Câu 17 (NB): Phương pháp: a) Vận dụng kiến thức về các trường hợp bằng nhau của tam giác. b) Chứng minh hai tam giác bằng nhau suy ra hai góc bằng nhau tương ứng. Sử dụng định lý hai góc đối đỉnh suy ra điều phải chứng minh. Cách giải: a) Chứng minh AB=CE và AB//CE. Xét ΔBAM và ΔCEM có : BM=MC (M là trung điểm của BC) MA=ME (cách vẽ) ^AMB=^CME (đối đỉnh) ⇒ΔABM=ΔECM(c−g−c) ⇒AB=CE (cặp cạnh tương ứng) Ta có : ^ABM=^ECM (cặp góc tương ứng) Mà hai góc đó là cặp góc so le trong nên AB//CE. b) Trên đoạn thẳng AB lấy điểm I và trên đoạn thẳng CE lấy điểm K sao cho AI=EK. Chứng minh rằng ba điểm I,M,K thẳng hàng. Từ câu a, ΔABM=ΔECM⇒^IAM=^KEM (góc tương ứng) Xét ΔAIM và ΔEKM có : AI=EK(gt) AM=ME(gt) ^IAM=^KEM(cmt) ⇒ΔAIM=ΔEKM(c−g−c) ⇒^IMA=^KME (cặp góc tương ứng) Do MA là tia đối của tia ME nên MI là tia đối của tia MK hay I,M,K thẳng hàng. Câu 18 (NB): Phương pháp: Áp dụng tính chất dãy tỉ số bằng nhau : Nếu ab=cd thì ad=bc. Và ab=cd=ef⇒ab=cd=ef=a+c+eb+d+f=a−c+eb−d+f Cách giải: Gọi hai số cần tìm là x và y (x,y≠0) Ta có : x+y5=x−y1=xy12 (*) Áp dụng tính chất dãy tỉ số bằng nhau ta có : x+y5=x−y1=x+y+x−y5+1=2x6=x3 Mà x+y5=x−y1=xy12 nên xy12=x3⇒xyx=123⇒y=4 Thay giá trị y=4 vào biểu thức (*) ta có : x+45=x−41⇒x+4=5x−20⇒24=4x⇒x=6 Vậy hai số cần tìm lần lượt là 6 và 4. Hết HocTot.Nam.Name.Vn
|