Giải đề thi học kì 1 toán lớp 7 năm 2019 - 2020 PGD Tân PhúGiải chi tiết đề thi học kì 1 môn toán lớp 7 năm 2019 - 2020 PGD Tân Phú với cách giải nhanh và chú ý quan trọng Bài 1: (1 điểm) Điền kí hiệu \( \in ;\) \( \notin ;\) hoặc \( \subset \) vào ô vuông để có phát biểu đúng : \( - 2019\,...N;\) \(Z...\,\,Q;\) \( - 6\,\,...\,Q;\) \(\sqrt 4 \,\,...N.\) Bài 2: (3,5 điểm) a) \(\dfrac{3}{2} \cdot x + \dfrac{1}{2} = \dfrac{5}{2}\) b) \(\left| {1 - x} \right| - \dfrac{1}{6} = {\left( {\dfrac{2}{3}} \right)^2}\) c)\(x = \dfrac{{19}}{{11}} \cdot \dfrac{5}{{14}} + \dfrac{1}{{11}} \cdot \dfrac{5}{7} - \sqrt {\dfrac{{25}}{4}} \cdot \dfrac{3}{{11}}\) d) \(x = \dfrac{{{{20}^{12}} \cdot {8^4} \cdot {3^{14}}}}{{{{15}^{13}} \cdot {2^{36}}}}\) Bài 3: (1,0 điểm) Tổng số học sinh tham gia Câu lạc bộ “Đàn dân tộc” của ba lớp \(7A,7B\) và \(7C\) là \(90\) học sinh. Biết số học sinh tham gia Câu lạc bộ của mỗi lớp \(7A,7B\) và \(7C\) lần lượt tỉ lệ với \(16,15\) và \(14\). Hỏi mỗi lớp có bao nhiêu học sinh tham gia câu lạc bộ trên. Bài 4: (1,0 điểm) Cho hình vẽ bên (học sinh không cần vẽ lại hình khi làm bài). a) Tính số đo của góc \(DEF.\) b) Hai tam giác trong hình có bằng nhau không ? Giải thích. Bài 5: (2,5 điểm) Cho tam giác nhọn \(ABC\) \(\left( {AB < AC} \right).\) Gọi \(D\) trung điểm của cạnh \(AC.\) Trên tia đối của tia \(DB\) lấy điểm \(E\) sao cho \(DE = DB.\) a) Chứng minh \(\Delta ABD = \Delta CED.\) Suy ra \(AB\) song song với \(CE.\) b) Kẻ \(AF\) vuông góc với \(BD\) tại \(F\) và \(CG\) vuông góc với \(DE\) tại \(G.\) Chứng minh \(AF\) song song với \(CG\) và \(DF = DG.\) c) Kẻ \(BH\) vuông góc với \(AD\) tại \(H\) và \(EI\) vuông góc với \(DC\) tại \(I.\) Đoạn \(BH\) cắt \(AF\) tại \(K.\) Đoạn \(CG\) cắt \(EI\) tại \(M.\) Chứng minh ba điểm \(K,D,M\) thẳng hàng. Bài 6: (1,0 điểm) Mẹ của An mang một số tiền vào siêu thị để mua hoa quả và nhẩm tính rằng với số tiền trên có thể mua được \(3kg\) lê, hoặc \(4kg\) nho, hoặc \(5kg\) táo. Tính giá tiền mỗi loại hoa quả trên, biết \(4kg\) nho đắt hơn \(3kg\) táo là \(240.000\) đồng. HƯỚNG DẪN GIẢI CHI TIẾT Thực hiện: Ban chuyên môn HocTot.Nam.Name.Vn
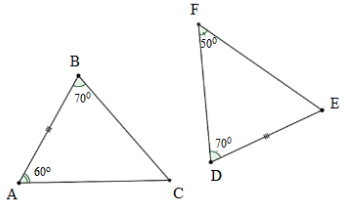
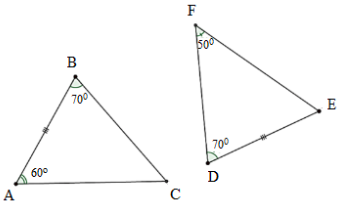
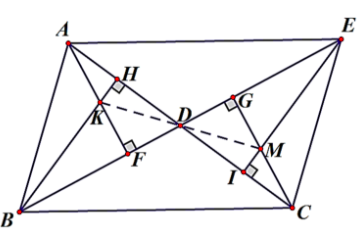
Bài 1 (VD): Phương pháp: Sử dụng \(N = \left\{ {0;1;2;3...} \right\}\), \(Z = \left\{ {...; - 2; - 1;0;1;2;...} \right\}\) Tập hợp \(Q\) gồm số hữu tỉ dạng \(\dfrac{a}{b}\,\,\left( {a,b \in Z,b \ne 0} \right)\) Cách giải: \( - 2019 \notin N;\) \(Z \subset Q;\) \( - 6 \in Q;\) \(\sqrt 4 \in N\,\) (vì \(\sqrt 4 = 2 \in N\)) Bài 2 (VD): Phương pháp: a) Sử dụng qui tắc chuyển vế đưa về dạng tìm \(x\) quen thuộc b) Tính lũy thừa trước rồi biến đổi về dạng \(\left| A \right| = m\,\left( {m \ge 0} \right)\) thì \(A = m\) hoặc \(A = - m.\) c) Tính căn thức, sử dụng tính chất phân phối của phép nhân đối với phép cộng d) Sử dụng các công thức lũy thừa: \({a^m}.{a^n} = {a^{m + n}};\,{a^m}:{a^n} = {a^{m - n}}\), \({\left( {{a^m}} \right)^n} = {a^{m.n}}\) , \({\left( {a.b} \right)^m} = {a^m}.{b^m}\) Cách giải: a) \(\dfrac{3}{2} \cdot x + \dfrac{1}{2} = \dfrac{5}{2}\) \(\dfrac{3}{2} \cdot x = \dfrac{5}{2} - \dfrac{1}{2}\) \(\dfrac{3}{2} \cdot x = 2\) \(x = 2:\dfrac{3}{2} = 2 \cdot \dfrac{2}{3} = \dfrac{4}{3}\) b) \(\left| {1 - x} \right| - \dfrac{1}{6} = {\left( {\dfrac{2}{3}} \right)^2}\) \(\left| {1 - x} \right| = \dfrac{4}{9} + \dfrac{1}{6}\) \(\left| {1 - x} \right| = \dfrac{{11}}{{18}}\) \(1 - x = \dfrac{{11}}{{18}}\) hoặc \(1 - x = - \dfrac{{11}}{{18}}\) \(x = 1 - \dfrac{{11}}{{18}}\) hoặc \(x = 1 - \left( { - \dfrac{{11}}{{18}}} \right)\) Nên \(x = \dfrac{7}{{18}}\) hoặc \(x = \dfrac{{29}}{{18}} \cdot \) c) \(x = \dfrac{{19}}{{11}} \cdot \dfrac{5}{{14}} + \dfrac{1}{{11}} \cdot \dfrac{5}{7} - \sqrt {\dfrac{{25}}{4}} \cdot \dfrac{3}{{11}}\) \(x = \dfrac{{19}}{{11}} \cdot \dfrac{5}{{14}} + \dfrac{1}{{11}} \cdot \dfrac{5}{7} - \dfrac{5}{2} \cdot \dfrac{3}{{11}}\) \(x = \dfrac{5}{{11}} \cdot \dfrac{{19}}{4} + \dfrac{5}{{11}} \cdot \dfrac{1}{7} - \dfrac{5}{{11}} \cdot \dfrac{3}{2}\) \(x = \dfrac{5}{{11}} \cdot \left( {\dfrac{{19}}{{14}} + \dfrac{1}{7} - \dfrac{3}{2}} \right)\) \(x = \dfrac{5}{{11}} \cdot \left( {\dfrac{{19}}{{14}} + \dfrac{2}{{14}} - \dfrac{{21}}{{14}}} \right)\) \(x = \dfrac{5}{{11}} \cdot 0 = 0\) d) \(x = \dfrac{{{{20}^{12}}{{.8}^4}{{.3}^{14}}}}{{{{15}^{13}}{{.2}^{36}}}}\) \( = \dfrac{{{{\left( {{2^2}.5} \right)}^{12}}.{{\left( {{2^3}} \right)}^4}{{.3}^{14}}}}{{{{\left( {3.5} \right)}^{13}}{{.2}^{36}}}}\) \( = \dfrac{{{2^{24}}{{.5}^{12}}{{.2}^{12}}{{.3}^{14}}}}{{{3^{13}}{{.5}^{13}}{{.2}^{36}}}}\) \( = \dfrac{{{2^{36}}{{.5}^{12}}{{.3}^{14}}}}{{{3^{13}}{{.5}^{13}}{{.2}^{36}}}} = \dfrac{3}{5}\) Bài 3 (VD ): Phương pháp: Gọi \(x,y,z\) lần lượt là số học sinh tham gia câu lạc bộ “Đàn dân tộc” của các lớp \(7A,7B,7C\) Từ đó lập dãy tỉ số bằng nhau và áp dụng tính chất dãy tỉ số bằng nhau. Cách giải: Gọi \(x,y,z\) lần lượt là số học sinh tham gia câu lạc bộ “Đàn dân tộc” của các lớp \(7A,7B,7C\) \(\left( {x,y,z \in \mathbb{N}*,0 < x,y,z < 90} \right).\) Theo đề bài : \(\dfrac{x}{{16}} = \dfrac{y}{{15}} = \dfrac{z}{{14}};\) \(x + y + z = 90\) Áp dụng tính chất của dãy tỉ số bằng nhau, ta được \(\dfrac{x}{{16}} = \dfrac{y}{{15}} = \dfrac{z}{{14}} = \dfrac{{x + y + z}}{{16 + 15 + 14}} = \dfrac{{90}}{{45}} = 2\) Do đó : \(\left\{ \begin{array}{l}\dfrac{x}{{16}} = 2 \Rightarrow x = 16.2 = 32\\\dfrac{y}{{15}} = 2 \Rightarrow y = 15.2 = 30\\\dfrac{z}{{14}} = 2 \Rightarrow z = 14.2 = 28\end{array} \right.\) Vậy số học sinh tham gia câu lạc bộ của các lớp \(7A,7B,7C\) thứ tự là \(32\) học sinh, \(30\) học sinh, \(28\) học sinh. Bài 4 (VD ): Phương pháp: a) Sử dụng định lý tổng ba góc trong tam giác bằng \({180^0}\) b) Chứng minh hai tam giác bằng nhau theo trường hợp góc cạnh góc Cách giải: a) Tính số đo của góc \(DEF.\) Xét tam giác \(DEF\) có \(\widehat {DEF} + \widehat {EDF} + \widehat {EFD} = 180^\circ \) (định lí tổng ba góc trong tam giác) \(\widehat {DEF} + 70^\circ + 50^\circ = 180^\circ \) Suy ra \(\widehat {DEF} = {180^0} - {70^0} - {50^0} = 60^\circ .\) b) Hai tam giác trong hình có bằng nhau không ? Giải thích. Xét \(\Delta ABC\) và \(\Delta EDF,\) có: \(\widehat B = \widehat D = 70^\circ \left( {gt} \right)\) \(AB = DE\left( {gt} \right)\) \(\widehat A = \widehat E = 60^\circ \left( {cmt} \right)\) Do đó, \(\Delta ABC = \Delta EDF\left( {g - c - g} \right).\) Bài 5 (VD ): Phương pháp: a) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh góc cạnh và sử dụng tính chất hai tam giác bằng nhau. b) Sử dụng quan hệ từ vuông góc đến song song và trường hợp bằng nhau cạnh huyền – góc nhọn của tam giác vuông c) Sử dụng tính chất trực tâm tam giác. Cách giải: Cho tam giác nhọn \(ABC\) \(\left( {AB < AC} \right).\) Gọi \(D\) trung điểm của cạnh \(AC.\) Trên tia đối của tia \(DB\) lấy điểm \(E\) sao cho \(DE = DB.\)
a) Chứng minh \(\Delta ABD = \Delta CED.\) Suy ra \(AB\) song song với \(CE.\) Xét tam giác \(ABD\) và tam giác \(CDE\) có: +) \(AD = DC\) (vì \(D\) là trung điểm cạnh \(AC\)) +) \(\widehat {ADB} = \widehat {EDC}\) (hai góc đối đỉnh) +) \(BD = DE\,\,\left( {gt} \right)\) Nên \(\Delta ADB = \Delta CDE\left( {c - g - c} \right).\) Suy ra \(\widehat {BAD} = \widehat {ECD}.\) Mà \(\widehat {BAD}\) và \(\widehat {ECD}\) ở vị trí so le trong Nên \(AB\) song song với \(CE.\) b) Kẻ \(AF\) vuông góc với \(BD\) tại \(F\) và \(CG\) vuông góc với \(DE\) tại \(G.\) Chứng minh \(AF\) song song với \(CG\) và \(DF = DG.\) Vì \(\left\{ \begin{array}{l}AF \bot BE\,\left( {gt} \right)\\CG \bot BE\left( {gt} \right)\end{array} \right.\) nên \(AF\) song song với \(CG\) (cùng vuông góc với \(BE\)) Suy ra \(\widehat {FAD} = \widehat {GCD}\) (hai góc ở vị trí so le trong) Xét tam giác \(AFD\) và tam giác \(CGD\) có: +) \(\widehat {AFD} = \widehat {CGD} = {90^0}\) +) \(AD = DC\,\left( {cmt} \right)\) +) \(\widehat {FAD} = \widehat {GCD}\,\left( {cmt} \right)\) Nên \(\Delta FAD = \Delta GCD\left( {ch - gn} \right).\) Suy ra \(DF = DG\) (hai cạnh tương ứng) c) Kẻ \(BH\) vuông góc với \(AD\) tại \(H\) và \(EI\) vuông góc với \(DC\) tại \(I.\) Đoạn \(BH\) cắt \(AF\) tại \(K.\) Đoạn \(CG\) cắt \(EI\) tại \(M.\) Chứng minh ba điểm \(K,D,M\) thẳng hàng. Xét tam giác \(ABD\) có hai đường cao \(AF\) và \(BH\) giao nhau tại \(K\) nên \(K\) là trực tâm tam giác \(ABD.\) Suy ra \(DK \bot AB\) mà \(AB//CE\) (theo câu a) nên \(DK \bot EC\) (1) Xét tam giác \(EDC\) có hai đường cao \(EI\) và \(CG\) giao nhau tại \(M\) nên \(M\) là trực tâm tam giác \(EDC.\) Suy ra \(DM \bot EC\)(2) Từ (1) và (2) suy ra \(K,D,M\) thẳng hàng. Bài 6 (VD ): Phương pháp: Sử dụng tính chất dãy tỉ số bằng nhau Cách giải: Gọi \(x,y,z\) (đơn vị : đồng) lần lượt là giá tiền của mỗi kg lê, nho, táo (\(x,y,z\) dương) Theo đề ta có: \(3x = 4y = 5z\) và \(4y - 3z = 240000\) Suy ra : \(\dfrac{{3x}}{{60}} = \dfrac{{4y}}{{60}} = \dfrac{{5z}}{{60}}\) và \(4y - 3z = 240000\) Hay \(\dfrac{x}{{20}} = \dfrac{y}{{15}} = \dfrac{z}{{12}}\) và \(4y - 3z = 240000\) Áp dụng tính chất dãy tỉ số bằng nhau : \(\dfrac{x}{{20}} = \dfrac{y}{{15}} = \dfrac{z}{{12}} = \dfrac{{4y - 3z}}{{4.15 - 3.12}} = \dfrac{{240000}}{{24}} = 10000\) Suy ra \(x = 200000;y = 150000;\,z = 120000.\) Vậy giá mỗi kg lê là \(200000\) đồng, mỗi kg nho giá \(150000\) đồng và mỗi kg táo giá \(120000\) đồng. HocTot.Nam.Name.Vn
|