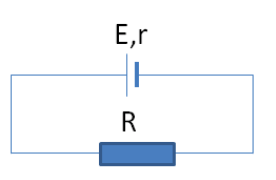
Giải đề thi học kì 1 lý lớp 11 năm 2019 - 2020 trường THPT Bắc Thăng Long

Câu 1: (2 điểm)

a) Trình bày bản chất dòng điện trong kim loại.

b) Viết công thức thể hiện sự phụ thuộc của điện trở suất của kim loại vào nhiệt độ, giải thích ý nghĩa của các đại lượng trong công thức.

Câu 2: (2 điểm)

Một mối hàn của một cặp nhiệt điện có hệ số \({\alpha _T} = 48\left( {\mu V/K} \right)\) được đặt trong không khí ở \({20^0}C\). Mối hàn còn lại được nung nóng đến nhiệt độ \({220^0}C\). Tính suất điện động nhiệt điện của cặp nhiệt điện khi đó.

Câu 3: (2 điểm)

Cho mạch điện như hình vẽ. Biết nguồn có suất điện động \(E = 12V\), điện trở trong \(r = 1\Omega \), điện trở \(R = 9\Omega \). Tính:

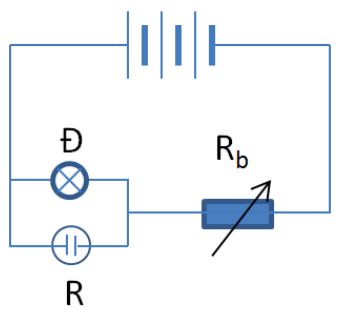
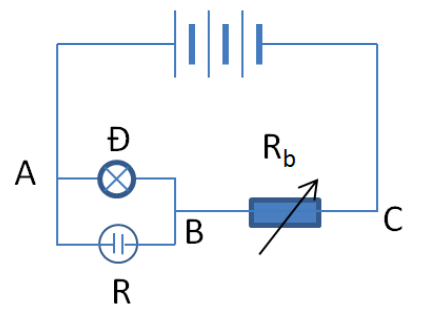
a. Cường độ dòng điện chạy qua mạch.

b. Hiệu suất của nguồn điện.

c. Công suất tỏa nhiệt của mạch ngoài.

Câu 4: (3,5 điểm)

Cho mạch điện như hình vẽ. Bộ nguồn gồm 3 nguồn giống nhau; mỗi nguồn có suất điện động bằng \(6V\), điện trở trong bằng \(0,2\Omega \). Mạch ngoài gồm bóng đèn sợi đốt loại \(6V - 9W\), bình điện phân dung dịch \(CuS{O_4}\), cực dương làm bằng đồng có điện trở \({R_P} = 6\Omega \), \({R_b}\) là biến trở.

1. Điều chỉnh để biến trở \({R_b} = 9\Omega \). Tính:

a. Cường độ dòng điện trong mạch chính.

b. Khối lượng đồng bám vào catot sau \(1\) giờ \(20\) phút (cho biết đối với đồng \(A = 64g/mol\), \(n = 2\))

c. Đèn sáng như thế nào? Vì sao?

2. Tìm \({R_b}\) để công suất tỏa nhiệt trên biến trở đạt giá trị lớn nhất. Tìm giá trị lớn nhất đó.

Câu 5: (0,5 điểm)

Mạch kín gồm nguồn điện \(E = 200V\), \(r = 0,5\Omega \) và hai điện trở \({R_1} = 100\Omega \) và \({R_2} = 500\Omega \) mắc nối tiếp. Một vôn kế không lí tưởng được mắc song song với \({R_2}\) thì số chỉ của nó là \(160V\). Tìm số chỉ của vôn kế nói trên nếu nó được mắc song song với \({R_1}\)

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn HocTot.Nam.Name.Vn 

Câu 1 (NB):

Phương pháp:

a) Xem lí thuyết về bản chất dòng điện trong kim loại SGK VL11 trang 74

b) Xem biểu thức sự phụ thuộc của điện trở suất của kim loại vào nhiệt độ SGK VL11 trang 75

Cách giải:

a) Bản chất dòng điện trong kim loại: Dòng điện trong kim loại là dòng dịch chuyển có hướng của các êlectron tự do ngược chiều điện trường.

b)

Công thức sự phụ thuộc của điện trở suất của kim loại vào nhiệt độ: \(\rho  = {\rho _0}\left[ {1 + \alpha \left( {t - {t_0}} \right)} \right]\)

Trong đó:

+ \({\rho _0}\): điện trở suất ở \({t_0}\) (thường lấy \({20^0}C\))

+ \(\alpha \): hệ số nhiệt điện trở

Câu 2 (VD):

Phương pháp:

Vận dụng biểu thức tính suất điện động nhiệt điện: \(E = {\alpha _T}\left( {{T_2} - {T_1}} \right)\)

Cách giải:

Suất điện động nhiệt điện của cặp nhiệt điện: \(E = {\alpha _T}\left( {{T_2} - {T_1}} \right) = {48.10^{ - 6}}.\left( {220 - 20} \right) = 9,{6.10^{ - 3}}V\)

Câu 3 (VD):

Phương pháp:

a) Sử dụng biểu thức định luật Ôm cho toàn mạch: \(I = \dfrac{E}{{R + r}}\)

b) Sử dụng biểu thức tính hiệu suất của nguồn: \(H = \dfrac{{{U_N}}}{E}.100\%  = \dfrac{R}{{R + r}}.100\% \)

c) Sử dụng biểu thức tính công suất: \(P = {I^2}R\)

Cách giải:

a) Cường độ dòng điện chạy trong mạch: \(I = \dfrac{E}{{R + r}} = \dfrac{{12}}{{9 + 1}} = 1,2A\)

b) Hiệu suất của nguồn điện:

\(H = \dfrac{{{U_N}}}{E}.100\%  = \dfrac{R}{{R + r}}.100\%  \\= \dfrac{9}{{9 + 1}}.100\%  = 90\% \)

c) Công suất tỏa nhiệt của mạch ngoài: \({P_N} = {I^2}R = 1,{2^2}.9 = 12,96W\)

Câu 4 (NB):

Phương pháp:

+ Áp dụng biểu thức: \(R = \dfrac{{{U^2}}}{P}\)

+ Sử dụng biểu thức tính bộ nguồn mắc nối tiếp: \(\left\{ \begin{array}{l}{E_b} = {E_1} + {E_2} + ...\\{r_b} = {r_1} + {r_2} + ...\end{array} \right.\)

1.

a)

+ Vận dụng biểu thức tính điện trở của mạch mắc song song: \(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\)

+ Vận dụng biểu thức tính điện trở của mạch mắc nối tiếp: \(R = {R_1} + {R_2}\)

+ Áp dụng biểu thức định luật ôm cho toàn mạch: \(I = \dfrac{E}{{{R_N} + r}}\)

b)

+ Áp dụng biểu thức của đoạn mạch mắc song song: \(U = {U_1} = {U_2}\)

+ Vận dụng biểu thức định luật ôm: \(I = \dfrac{U}{R}\)

+ Sử dụng biểu thức định luật Fa-ra-day: \(m = \dfrac{1}{F}\dfrac{A}{n}It\)

c)

+ Vận dụng biểu thức: \(P = UI\)

+ So sánh cường độ dòng điện chạy qua đèn với cường độ dòng điện định mức của đèn

2.

+ Áp dụng biểu thức tính công suất: \(P = {I^2}R\)

+ Vận dụng biểu thức Cosi

Cách giải:

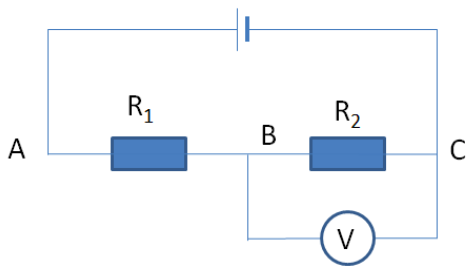
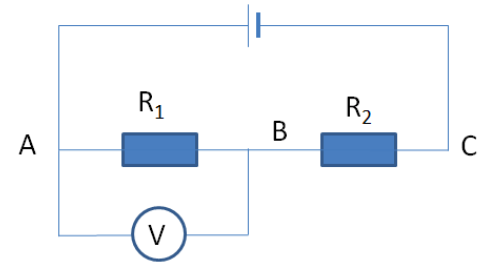
Ta có:

+ Hiệu điện thế định mức của đèn và công suất định mức của đèn: \(\left\{ \begin{array}{l}{U_{dm}} = 6V\\{P_{dm}} = 9W\end{array} \right.\)

\( \Rightarrow \) Điện trở của đèn: \({R_D} = \dfrac{{U_{dm}^2}}{{{P_{dm}}}} = \dfrac{{{6^2}}}{9} = 4\Omega \)

+ Mạch gồm 3 nguồn mắc nối tiếp với nhau

\( \Rightarrow \) Suất điện động của bộ nguồn: \({\xi _b} = 3\xi  = 3.6 = 18V\)

Điện trở trong của bộ nguồn: \({r_b} = 3r = 3.0,2 = 0,6\Omega \)

1.

a)

Ta có: \(\left[ {{R_D}//{R_P}} \right]ntR{ _b}\)

\({R_{AB}} = \dfrac{{{R_D}{R_P}}}{{{R_D} + {R_P}}} = \dfrac{{4.6}}{{4 + 6}} = 2,4\Omega \)

Điện trở tương đương mạch ngoài: \({R_N} = {R_{AB}} + {R_b} = 2,4 + 9 = 11,4\Omega \)

Cường độ dòng điện chạy trong mạch chính: \(I = \dfrac{{{\xi _b}}}{{{R_N} + {r_b}}} = \dfrac{{18}}{{11,4 + 0,6}} = 1,5A\)

b)

Ta có: \({U_{AB}} = I.{R_{AB}} = 1,5.2,4 = 3,6V\)

Cường độ dòng điện qua bình điện phân: \({I_P} = \dfrac{{{U_P}}}{{{R_P}}} = \dfrac{{{U_{AB}}}}{{{R_P}}} = \dfrac{{3,6}}{6} = 0,6A\) 

Khối lượng đồng bám vào catot sau thời gian \(t = 1h20' = 4800s\)  là:

\(m = \dfrac{1}{F}\dfrac{A}{n}{I_P}t = \dfrac{1}{{96500}}\dfrac{{64}}{2}.0,6.4800 \\= 0,955g\)

c)

Cường độ dòng điện chạy qua đèn: \({I_D} = \dfrac{{{U_D}}}{{{R_D}}} = \dfrac{{{U_{AB}}}}{{{R_D}}} = \dfrac{{3,6}}{4} = 0,9A\)

Ta có, cường độ dòng điện định mức của đèn: \({I_{dm}} = \dfrac{{{P_{dm}}}}{{{U_{dm}}}} = \dfrac{9}{6} = 1,5A\)

Nhận thấy \({I_D} < {I_{dm}} \Rightarrow \) Đèn sáng yếu hơn bình thường.

2.

+ Điện trở tương đương mạch ngoài: \({R_N} = {R_{AB}} + {R_b} = 2,4 + {R_b}\)

Cường độ dòng điện qua mạch: \(I = \dfrac{{{\xi _b}}}{{{R_N} + {r_b}}} = \dfrac{{18}}{{2,4 + {R_b} + 0,6}} \\= \dfrac{{18}}{{3 + {R_b}}}\)

Công suất tỏa nhiệt trên biến trở: \(P = {I^2}{R_b} = \dfrac{{{{18}^2}}}{{{{\left( {3 + {R_b}} \right)}^2}}}{R_b} \\= \dfrac{{324}}{{{{\left( {\dfrac{3}{{\sqrt {{R_b}} }} + \sqrt {{R_b}} } \right)}^2}}}\)

Công suất \(P\)cực đại khi \({\left( {\dfrac{3}{{\sqrt {{R_b}} }} + \sqrt {{R_b}} } \right)^2}_{\min }\)

Ta có: \(\left( {\dfrac{3}{{\sqrt {{R_b}} }} + \sqrt {{R_b}} } \right) \ge 2\sqrt 3 \)

\({\left( {\dfrac{3}{{\sqrt {{R_b}} }} + \sqrt {{R_b}} } \right)^2}_{\min } = 12\) khi \(\dfrac{3}{{\sqrt {{R_b}} }} = \sqrt {{R_b}}  \Rightarrow {R_b} = 3\Omega \)

Khi đó: \({P_{max}} = \dfrac{{324}}{{12}} = 27W\)  

Câu 5 (NB):

Phương pháp:

+ Vận dụng biểu thức tính điện trở của mạch gồm các điện trở mắc nối tiếp: \(R = {R_1} + {R_2}\)

+ Vận dụng biểu thức tính điện trở của mạch gồm các điện trở mắc song song: \(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\)

+ Áp dụng biểu thức định luật ôm cho toàn mạch: \(I = \dfrac{E}{{R + r}}\)

Cách giải:

Vôn kế không lí tưởng suy ra vôn kế có điện trở \({R_V}\) hữu hạn.

+ Ban đầu, khi vôn kế mắc song song với \({R_2}\):

Mạch của ta gồm: \({R_1}nt\left( {{R_2}//{R_V}} \right)\)

\({R_{2V}} = \dfrac{{{R_2}{R_V}}}{{{R_2} + {R_V}}} = \dfrac{{500{R_V}}}{{500 + {R_V}}}\)

\({R_N} = {R_1} + {R_{2V}} = 100 + \dfrac{{500{R_V}}}{{500 + {R_V}}}\)

Cường độ dòng điện qua mạch: \(I = \dfrac{E}{{{R_N} + r}}\)

\(\begin{array}{l}{U_V} = {U_{BC}} = I.{R_{2V}}\\ \Leftrightarrow 160 = \dfrac{{200}}{{100 + \dfrac{{500{R_V}}}{{500 + {R_V}}} + 0,5}}\left( {\dfrac{{500{R_V}}}{{500 + {R_V}}}} \right)\\ \Rightarrow {R_V} = 2051\Omega \end{array}\)

+ Khi vôn kế mắc song song với \({R_1}\) :

Mạch gồm: \(\left( {{R_1}//{R_V}} \right)nt{R_2}\)

\({R_{1V}} = \dfrac{{{R_1}{R_V}}}{{{R_1} + {R_V}}} = 95,35\Omega \)

Điện trở tương đương mạch ngoài: \(R = {R_{1V}} + {R_2} = 595,35\Omega \)

Cường độ dòng điện trong mạch: \(I = \dfrac{E}{{R + r}} = \dfrac{{200}}{{595,35 + 0,5}} = 0,336A\)

Số chỉ của vôn kế:

\({U_V} = {U_{AB}} = I.{R_{1V}} = 0,336.95,35 = 32,04V\) 

HocTot.Nam.Name.Vn