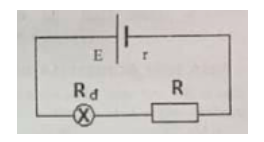
Giải đề thi học kì 1 lý lớp 11 năm 2019 - 2020 sở Vĩnh Phúc

 I. PHẦN TRẮC NGHIỆM (3,0 điểm).

Câu 1. Xét một mạch điện kín gồm nguồn điện có suất điện động \(E\) , điện trở trong  \(r\) và điện trở mạch ngoài \({R_N}\). Hiệu điện thế mạch ngoài được xác định bởi biểu thức nào sau đây?

A. \({U_N} = I.r\)

B. \({U_N} = I\left( {{R_N} + r} \right)\)

C. \({U_N} = E - I.r\)

D. \({U_N} = E + I.r\)

Câu 2. Điện trường là

A. môi trường bao quanh điện tích, có thể làm cho bóng đèn sợi đốt nóng sáng.

B. môi trường dẫn điện và có rất nhiều các điện tích tự do.

C. môi trường chứa các điện tích.

D. môi trường bao quanh điện tích, gắn với điện tích và tác dụng lực điện lên các điện tích khác đặt trong nó.

Câu 3. Hai điện tích điểm \({q_1}\) và \({q_2}\) khi đặt gần nhau thì chúng đẩy nhau. Kết luận nào sau đây là đúng?

A. \({q_1}\) đặt rất gần \({q_2}\)

B. \({q_1}\) cùng dấu với  \({q_2}\)

C. \({q_1}\) dương, \({q_2}\) âm

D. \({q_1}\) âm, \({q_2}\) dương

Câu 4. Điện dung của tụ điện có đơn vị là

A. Vôn (V)                 B. Oát (W)

C. Fara (F)                D. Ampe (A)

Câu 5. Mắc nối tiếp 3 pin giống nhau, biết mỗi pin có suất điện động 3V và điện trở trong \(1\Omega \). Suất điện động và điện trở trong của bộ pin là

A. 9V và \(9\Omega \)                       B. 9V và \(3\Omega \)

C. 3V và \(9\Omega \)                       D. 3V và \(3\Omega \)

Câu 6. Mối liên hệ giữa hiệu điện thế \({U_{MN}}\) và hiệu điện thế \({U_{NM}}\) là

A. \({U_{MN}} = {U_{NM}}\)

B. \({U_{MN}} = \dfrac{1}{{{U_{NM}}}}\)

C. \({U_{MN}} =  - {U_{NM}}\)

D. \({U_{MN}} =  - \dfrac{1}{{{U_{NM}}}}\)

Câu 7. Phát biểu nào sau đây không đúng khi nói về tác dụng của dòng điện?

A. Acquy làm cho bóng đèn sợi đốt sáng lên biểu hiện tác dụng hóa học của dòng điện

B. Nam châm điện là một ví dụ về tác dụng từ của dòng điện

C. Hiện tượng điện giật là một tác dụng sinh lý của dòng điện.

D. Bàn là hoạt động dựa trên tác dụng nhiệt của dòng điện.

Câu 8. Trên một bóng đèn có ghi 220V – 100W. Công suất tiêu thụ định mức của bóng đèn là

A. 100W                     B. 220W

C. 120W                     D. 320W

Câu 9. Một điện tích điểm \(Q\), cường độ điện trường tại một điểm trong chân không, cách điện tích Q một khoảng \(r\) có độ lớn được xác định bởi biểu thức nào sau đây?

A. \(E = {9.10^9}.\dfrac{{\left| Q \right|}}{{{r^3}}}\)

B. \(E = {9.10^9}.\dfrac{{\left| Q \right|}}{{\sqrt r }}\)

C. \(E = {9.10^9}.\dfrac{{\left| Q \right|}}{r}\)

D. \(E = {9.10^9}.\dfrac{{\left| Q \right|}}{{{r^2}}}\)

Câu 10. Phát biểu nào sau đây không đúng?

A. Electron là hạt mang điện tích âm, có độ lớn \(1,{6.10^{ - 19}}C\).

B. Electron là hạt có khối lượng \(m = 9,{1.10^{ - 31}}kg\).

C. Nguyên tử có thể mất hoặc nhận thêm electron để trở thành ion.

D. Electron không thể chuyển động từ vật này sang vật khác.

Câu 11. Vật bị nhiễm điện do cọ xát vì khi cọ xát

A. electron chuyển từ vật này sang vật khác

B. vật bị nóng lên

C. Các đinẹ tích tự đo được tạo ra trong vật

D. các điện tích bị mất đi

Câu 12. Một nguồn điện có suất điện động E, dòng điện qua nguồn có cường độ I, thời gian dòng điện qua mạch là t. Công suất của nguồn điện được xác định theo công thức

A. P = UI                    B. P = EI                     C. P = UIt                   D. P = EIt

II. PHẦN TỰ LUẬN (7,0 điểm).

Câu 13: (2,0 điểm) Cho mạch điện như hình vẽ. Biết nguồn điện có suất điện động E = 6V, điện trở trong của nguồn r = 0,1Ω; các điện trở R_đ = 11 Ω; R = 0,9 Ω.

a) Viết công thức tính điện trở tương đương của mạch ngoài. Áp dụng số liệu đề bài đã cho để tính điện trở tương đương của mạch ngoài.

b) Tính cường độ dòng điện qua mạch.

Câu 14: (2,5 điểm)

a)  Viết công thức của định luật Jun – Len xơ và giải thích các đại lượng có trong công thức của định luật.

b) Một bóng đèn sợi đốt loại (6V – 6W). Tính nhiệt lượng do bóng đèn này tỏa ra trong thời gian 20 phút, biết đèn sáng bình thường.

c) Mắc nối tiếp bóng đèn trên với biến trở R_x và đặt vào hai đầu mạch một nguồn điện có suất điện động 14V, điện trở trong r = 1Ω. Tìm giá trị của R_x để công suất tiêu thụ trên R_x  đạt giá trị cực đại. Tính công suất cực đại đó.

Câu 15: (2,5 điểm) Có hai điện tích điểm \({q_1} = q = {4.10^{ - 9}}C\) và \({q_2} = 4q = {16.10^{ - 9}}C\) đặt cách nhau một khoảng r = 1cm trong không khí.

a) Tính độ lớn lực tương tác giữa hai điện tích này.

b) Cần đặt điện tích thứ ba \({q_0}\) ở đâu, có dấu và độ lớn như thế nào để hệ ba điện tích trên nằm cân bằng? Biết hai điện tích \({q_1}\) và \({q_2}\) để tự do.

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn HocTot.Nam.Name.Vn

I. PHẦN TRẮC NGHIỆM

Câu 1 (NB):

Phương pháp:

Sử dụng lí thuyết về định luật ôm đối với toàn mạch

Cách giải:

Hiệu điện thế mạch ngoài được xác định bởi biểu thức: \(U = E - Ir\)

Chọn C

Câu 2 (NB):

Phương pháp:

Sử dụng lí thuyết về điện trường SGK VL11 trang 15

Cách giải:

Điện trường là một dạng vật chất (môi trường) bao quanh điện tích và gắn liền với điện tích. Điện trường tác dụng lực điện lên các điện tích khác đặt trong nó.

Chọn D

Câu 3 (TH):

Phương pháp:

Vận dụng sự tương tác của 2 điện tích:

+ Hai điện tích cùng dấu thì đẩy nhau

+ Hai điện tích khác dấu thì hút nhau

Cách giải:

Ta có, 2 diện tích \({q_1},{q_2}\) đẩy nhau \( \Rightarrow {q_1}.{q_2} > 0\) hay nói cách khác \({q_1}\), \({q_2}\) cùng dấu.

Chọn B

Câu 4 (NB):

Phương pháp:

Sử dụng lí thuyết về tụ điện

Cách giải:

Đơn vị của điện dung (C) là Fara (F)

Chọn C

Câu 5 (VD):

Phương pháp:

Sử dụng biểu thức của bộ nguồn mắc nối tiếp: \(\left\{ \begin{array}{l}{E_b} = {E_1} + {E_2}\\{r_b} = {r_1} + {r_2}\end{array} \right.\)

Cách giải:

Suất điện động của bộ nguồn: \({E_b} = {E_1} + {E_2} + {E_3} = 3E = 3.3 = 9V\)

Điện trở trong của bộ nguồn: \({r_b} = {r_1} + {r_2} + {r_3} = 3r = 3.1 = 3\Omega \)

Chọn B

Câu 6 (TH):

Phương pháp:

Vận dụng lí thuyết về hiệu điện thế

Cách giải:

Mối liên hệ giữa \({U_{MN}}\) và \({U_{NM}}\) là: \({U_{MN}} =  - {U_{NM}}\)

Chọn C

Câu 7 (TH):

Phương pháp:

Vận dụng lí thuyết về các tác dụng của dòng điện

Cách giải:

A – sai vì đó là biểu hiện tác dụng quang của dòng điện

B, C, D - đúng

Chọn A

Câu 8 (NB):

Phương pháp:

Đọc thông số trên dụng cụ tiêu thụ điện

Cách giải:

Ta có bóng đèn ghi \(220V - 100W\)

\( \Rightarrow \) Hiệu điện thế định mức của đèn \(220V\) và công suất định mức của đèn \(100W\)

Chọn A

Câu 9 (NB):

Phương pháp:

Sử dụng biểu thức xác định cường độ điện trường của một điện tích

Cách giải:

Cường độ điện trường của một điện tích điểm: \(E = k\dfrac{{\left| Q \right|}}{{{r^2}}} = {9.10^9}\dfrac{{\left| Q \right|}}{{{r^2}}}\)

Chọn D

Câu 10 (TH):

Phương pháp:

Vận dụng thuyết electron

Cách giải:

A, B, C – đúng

D – sai vì: Electron có thể di chuyển từ vật này sang vật khác

Chọn D

Câu 11 (TH):

Phương pháp:

Vận dụng thuyết electron giải thích các hiện tượng nhiễm điện

Cách giải:

Vật bị nhiễm điện do cọ xát vì khi cọ xát các electron di chuyển từ vật này sang vật khác.

Chọn A

Câu 12 (NB):

Phương pháp:

Sử dụng lí thuyết về công suất của nguồn điện

Cách giải:

Công suất của nguồn điện: \(P = EI\)

Chọn B

II. PHẦN TỰ LUẬN

Câu 13 (VD):

Phương pháp:

a) Sử dụng biểu thức tính điện trở tương đương của đoạn mạch có các điện trở mắc nối tiếp: \(R = {R_1} + {R_2}\)

b) Áp dụng biểu thức định luật Ôm cho toàn mạch: \(I = \dfrac{E}{{R + r}}\)

Cách giải:

a) Ta có mạch ngoài gồm \({R_d}ntR\)

\( \Rightarrow \) Điện trở tương đương mạch ngoài: \(R = {R_d} + R = 11 + 0,9 = 11,9\Omega \)

b) Cường độ dòng điện qua mạch: \(I = \dfrac{E}{{R + r}} = \dfrac{6}{{11,9 + 0,1}} = 0,5A\)

Câu 14 (VD):

Phương pháp:

a) Sử dụng biểu thức định luật Jun – Len xơ SGK VL11 trang 47

b) Sử dụng biểu thức tính nhiệt lượng: \(Q = {I^2}Rt = Pt\)

c)

+  Sử dụng biểu thức định luật Ôm cho toàn mạch: \(I = \dfrac{E}{{R + r}}\)

+ Sử dụng biểu thức tính công suất: \(P = {I^2}R\)

+ Áp dụng BĐT Cosi

Cách giải:

a) Biểu thức định luật Jun-Len xơ: \(Q = {I^2}Rt\)

Trong đó:

+ \(Q\): Nhiệt lượng tỏa ra

+ \(I\): Cường độ dòng điện

+ \(R\): Điện trở của vật dẫn

+ \(t\): Thời gian dòng điện chạy qua vật dẫn

b) Nhiệt lượng đèn tỏa ra trong thời gian \(t = 20' = 20.60 = 1200s\) là:

\(Q = Pt = 6.1200 = 7200J\)

c)

+ Điện trở của đèn: \({R_d} = \dfrac{{U_{dm}^2}}{{{P_{dm}}}} = \dfrac{{{6^2}}}{6} = 6\Omega \)

+ Điện trở tương đương mạch ngoài: \(R = {R_d} + {R_x} = 6 + {R_x}\)

+ Cường độ dòng điện qua mạch: \(I = \dfrac{E}{{R + r}} = \dfrac{{14}}{{6 + {R_x} + 1}} = \dfrac{{14}}{{7 + {R_x}}}\)

+ Công suất tiêu thụ trên \({R_x}\): \(P = {I^2}{R_x} = \dfrac{{{{14}^2}}}{{{{\left( {7 + {R_x}} \right)}^2}}}.{R_x} \\= \dfrac{{196}}{{{{\left( {\dfrac{7}{{\sqrt {{R_x}} }} + \sqrt {{R_x}} } \right)}^2}}}\)

\({P_{max}}\) khi \({\left( {\dfrac{7}{{\sqrt {{R_x}} }} + \sqrt {{R_x}} } \right)^2}_{\min }\)

Ta có: \({\left( {\dfrac{7}{{\sqrt {{R_x}} }} + \sqrt {{R_x}} } \right)^2} \ge {\left( {2\sqrt 7 } \right)^2} = 28\)

Dấu “=” xảy ra khi \(\dfrac{7}{{\sqrt {{R_x}} }} = \sqrt {{R_x}}  \Rightarrow {R_x} = 7\Omega \)

\({P_{max}} = \dfrac{{196}}{{28}} = 7{\rm{W}}\)  

Câu 15 (VD):

Phương pháp:

a) Sử dụng biểu thức định luật Cu-lông: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

b) Vận dụng điều kiện cân bằng của điện tích: \(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + ... = \overrightarrow 0 \)

Cách giải:

a)

Lực tương tác giữa hai điện tích: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = {9.10^9}\dfrac{{\left| {{{4.10}^{ - 9}}{{.16.10}^{ - 9}}} \right|}}{{0,{{01}^2}}} \\= 5,{76.10^{ - 3}}N\)

b)

\({q_1}\) đặt tại A, \({q_2}\) đặt tại B, \({q_0}\) tại C

- Gọi lực do \({q_1}\) tác dụng lên \({q_3}\) là \({F_{13}}\);   lực do \({q_2}\) tác dụng lên \({q_3}\) là \[{F_{23}}\)

- Để \({q_3}\) nằm cân bằng: \(\overrightarrow {{F_{13}}}  =  - \overrightarrow {{F_{23}}} \)

- Do \({q_1},{q_2}\) cùng dấu \( \Rightarrow {q_0}\) nằm trong khoảng \(AB\)

Lại có : \({F_{10}} = {F_{20}} \Leftrightarrow k\dfrac{{\left| {{q_1}{q_0}} \right|}}{{A{C^2}}} = k\dfrac{{\left| {{q_2}{q_0}} \right|}}{{B{C^2}}}\)

\( \Rightarrow \dfrac{{A{C^2}}}{{B{C^2}}} = \left| {\dfrac{{{q_1}}}{{{q_2}}}} \right| = \dfrac{1}{4}\)

\( \Rightarrow BC = 2AC\)    (1)

Lại có : \(AC + BC = 1cm\) (2)

Từ (1) và (2) ta suy ra : \(\left\{ \begin{array}{l}AC = \dfrac{1}{3}cm\\BC = \dfrac{2}{3}cm\end{array} \right.\)

- Gọi \(\overrightarrow {{F_{01}}} ,\overrightarrow {{F_{21}}} \) lần lượt là lực do \({q_0},{q_2}\) tác dụng lên \({q_1}\)

+ Điều kiện cân bằng của \({q_1}\): \(\overrightarrow {{F_{01}}}  + \overrightarrow {{F_{21}}}  = \overrightarrow 0 \)

\( \Rightarrow \overrightarrow {{F_{01}}}  =  - \overrightarrow {{F_{21}}} \) (3)

\( \Rightarrow \overrightarrow {{F_{01}}} \) ngược chiều \(\overrightarrow {{F_{21}}} \)

Ta suy ra, \({F_{01}}\) là lực hút

\( \Rightarrow {q_0} < 0\)

+ Lại có: \({F_{01}} = {F_{21}}\)

\(\begin{array}{l} \Leftrightarrow k\dfrac{{\left| {{q_0}{q_1}} \right|}}{{A{C^2}}} = k\dfrac{{\left| {{q_2}{q_1}} \right|}}{{A{B^2}}}\\ \Rightarrow \left| {{q_0}} \right| = \left| {{q_2}} \right|\dfrac{{A{C^2}}}{{A{B^2}}} = {16.10^{ - 9}}\dfrac{{{{\left( {\dfrac{1}{3}} \right)}^2}}}{{{1^2}}} \\= \dfrac{{16}}{9}{.10^{ - 9}}C\end{array}\)

\( \Rightarrow {q_3} =  - \dfrac{{16}}{9}{.10^{ - 9}}C\)  (do lập luận suy ra \({q_0} < 0\) ở trên) (3)

- Gọi \(\overrightarrow {{F_{02}}} ,\overrightarrow {{F_{12}}} \) lần lượt là lực do \({q_0},{q_1}\) tác dụng lên \({q_2}\)

+ Điều kiện cân bằng của \({q_1}\): \(\overrightarrow {{F_{02}}}  + \overrightarrow {{F_{12}}}  = \overrightarrow 0 \)

\( \Rightarrow \overrightarrow {{F_{02}}}  =  - \overrightarrow {{F_{12}}} \)

\( \Rightarrow \overrightarrow {{F_{02}}} \) ngược chiều \(\overrightarrow {{F_{12}}} \)

\( \Rightarrow {F_{02}}\) là lực hút

\( \Rightarrow {q_0} < 0\)

Lại có: \({F_{02}} = {F_{12}}\)

\(\begin{array}{l} \Leftrightarrow k\dfrac{{\left| {{q_0}{q_2}} \right|}}{{C{B^2}}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{A{B^2}}}\\ \Rightarrow \left| {{q_0}} \right| = \left| {{q_1}} \right|\dfrac{{C{B^2}}}{{A{B^2}}} = {4.10^{ - 9}}\dfrac{{{{\left( {\dfrac{2}{3}} \right)}^2}}}{{{1^2}}} \\= \dfrac{{16}}{9}{.10^{ - 9}}C\end{array}\)

\( \Rightarrow {q_3} =  - \dfrac{{16}}{9}{.10^{ - 9}}C\)  (do lập luận suy ra \({q_0} < 0\) ở trên) (4)

Vậy với \({q_3} =  - \dfrac{{16}}{9}{.10^{ - 9}}C\) thì hệ 3 điện tích cân bằng.

HocTot.Nam.Name.Vn