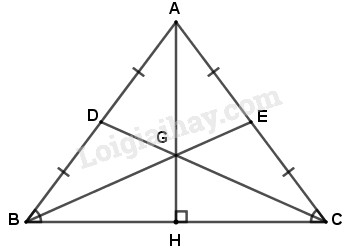
Đề kiểm tra 45 phút chương 3 phần Hình học 7 - Đề số 2Đề kiểm tra 45 phút chương 3: Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác đề số 2 trang 107 VBT lớp 7 tập 2 có đáp án, lời giải chi tiết kèm phương pháp giải đầy đủ tất cả các bài Đề bài Câu 1. (1 điểm) Cho tam giác ABC, trong đó AB<AC<BC. Khi đó, ta có (A) ˆC là góc lớn nhất; (B) ˆC là góc tù; (C) ˆC là góc vuông; (D) ˆC là góc nhọn. Câu 2. (1 điểm) Cho biết ba cạnh của một tam giác có số đo là những số nguyên. Nếu hai cạnh của tam giác đó có số đo là 2 và 5 thì cạnh thứ ba không thể có số đo là : (A) 8; (B) 6; (C) 5; (D) 4. Câu 3. (1 điểm) Cho tam giác ABC cân tại đỉnh A và không là tam giác đều. Gọi G là trọng tâm của tam giác đó. Ta có: (A) GA=GB; (B) GA=BC; (C) GB=GC; (D) GA=GB=GC Câu 4. (7 điểm) Cho tam giác ABC có đường trung tuyến AM bằng cạnh AB. Gọi H là trung điểm của BM và D là điểm sao cho H là trung điểm của AD. Chứng minh rằng a) AH⊥BC (1 điểm); b) Tam giác ACD là tam giác cân (1 điểm); c) M là trọng tâm của tam giác ACD (2 điểm); d) Đường thẳng DM đi qua trung điểm của cạnh AC và DM//AB (3 điểm). Lời giải chi tiết Câu 1: Phương pháp giải: Áp dụng kiến thức về quan hệ giữa góc và cạnh đối diện của một tam giác. Cách giải: Tam giác ABC có cạnh AB là nhỏ nhất nên góc C là góc bé nhất. Vậy ˆC là góc nhọn. Chọn D. Câu 2: Phương pháp giải: Vận dụng kiến thức về bất đẳng thức tam giác : Số đo một cạnh của tam giác phải nhỏ hơn tổng số đo hai cạnh còn lại. Cách giải: Ta có 2+5=7 mà 8>7 nên cạnh thứ ba không thể có số đo là 8. Chọn A. Câu 3: Phương pháp giải: Vận dụng kiến thức: Trong tam giác cân, đường trung tuyến ứng với hai cạnh bên bằng nhau thì bằng nhau. Cách giải:
ΔABC có GC=23DC; GB=23BE mà DC=BE. Vậy GB=GC. Chọn C.
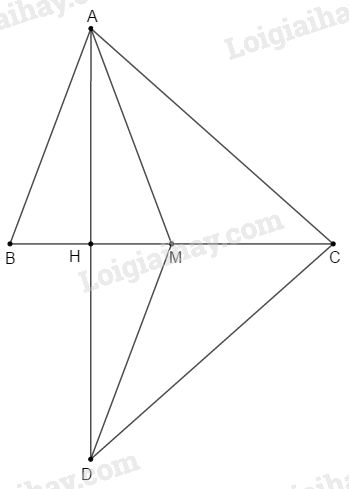
Câu 4: Phương pháp giải: a) Vận dụng kiến thức: Trong tam giác cân, đường trung tuyến hạ từ đỉnh đồng thời là đường cao của tam giác đó. b) Chứng minh tam giác có đường trung tuyến kẻ từ một đỉnh đồng thời là đường cao thì tam giác đó là tam giác cân. c) Chứng minh M nằm trên đường trung tuyến CH và MC=23CH d) Dựa vào tính chất ba đường trung tuyến của một tam giác đồng quy tại một điểm. Chứng minh cặp góc so le trong bằng nhau. Cách giải:
a) Tam giác ABM có AM=AB nên cân tại A. H là trung điểm của MB nên AH là đường trung tuyến của cạnh MB trong ΔABM ⇒AH⊥BM (tam giác cân có đường trung tuyến kẻ từ đỉnh đồng thời là đường cao). b) Xét tam giác ACD có CH⊥AD (chứng minh a) và AH=AD (theo cách vẽ điểm D) Suy ra, CH đồng thời là đường cao và đường trung tuyến trong tam giác ACD. Vậy ΔACD là tam giác cân tại C (tam giác có đường trung tuyến kẻ từ một đỉnh đồng thời là đường cao thì tam giác đó là tam giác cân) c) ΔABC có MC=12BC và MH=12MB=14BC Suy ra : MCMH=12BC14BC=2 hay MC=23CH Tam giác ACD có CH là đường trung tuyến; M∈CH và MC=23CH nên M là trọng tâm của ΔACD. d) Vì M là trọng tâm của ΔACD nên kéo dài DM ta được đường trung tuyến của cạnh AC hay DM đi qua trung điểm của AC. ΔACD là tam giác cân nên CH là đường cao đồng thời là đường trung trực của tam giác đó. Mà M∈CH nên MA=MD (tính chất đường trung trực của một đoạn thẳng) Xét hai tam giác vuông DMH và ABH có : HD=HA (cách vẽ) DM=AB (cùng bằng cạnh AM) Vậy ΔDMH=ΔABH (cạnh huyền – cạnh góc vuông) Suy ra ^MDH=^BAH (cặp góc tương ứng) Mà hai góc này ở vị trí so le trong nên DM//AB. HocTot.Nam.Name.Vn
|