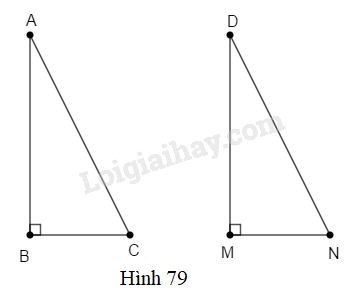
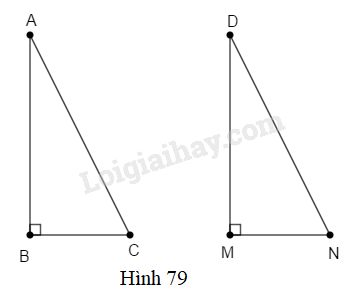
Đề kiểm tra 45 phút chương 2 phần Hình học 7 - Đề số 2Đề kiểm tra 45 phút chương 2: Tam giác đề số 2 trang 144 VBT lớp 7 tập 1 có đáp án, lời giải chi tiết kèm phương pháp giải đầy đủ tất cả các bài Đề bài Câu 1. (1 điểm) Đúng ghi Đ, sai ghi S vào ô trống trong mỗi khẳng định sau: a) Trong một tam giác, không thể có hai góc tù. ◻ b) Góc ngoài của một tam giác phải là góc tù. ◻ Câu 2. (1 điểm) Một tam giác vuông cân có cạnh góc vuông bằng 2dm. Độ dài cạnh huyền bằng: (A)4dm(B)√8dm(C)8dm(D)3dm Khoanh tròn vào chữ cái trước câu trả lời đúng. Câu 3. (1 điểm) Cho hình 79.
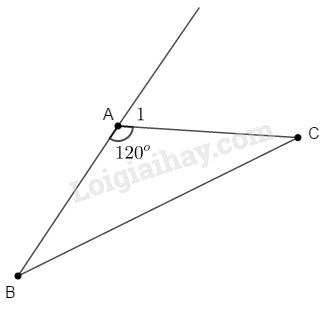
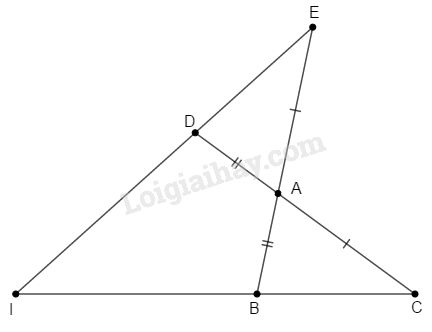
ΔABC=ΔDMN nếu có thêm điều kiện: (A)ˆC=ˆN(B)BC=MN(C)AB=BC(D)ˆA=45o Khoanh tròn vào chữ cái trước câu trả lời đúng. Câu 4. (2 điểm) Nêu các cách chứng minh một tam giác là tam giác cân. Câu 5. (5 điểm) Cho tam giác ABC(AB<AC). Trên tia đối của tia AB lấy điểm E, trên tia đối của tia AC lấy điểm D sao cho AE=AC;AD=AB. Các tia ED và CB cắt nhau tại I. Chứng minh rằng: a)BC=DEb)^ABI=^ADIc)IB=ID. Lời giải chi tiết Câu 1: Phương pháp: Định lí tổng ba góc của một tam giác bằng 180o. Lời giải: a) Đ Giả sử ΔABC có ˆA;ˆB là góc tù; tức là ˆA>90o;ˆB>90o. Do đó ˆA+ˆB>90o+90o=180o (mâu thuẫn định lí tổng ba góc của một tam giác). Vậy trong một tam giác, không thể có hai góc tù. b) S Ví dụ: ΔABC:ˆA=120o. Góc ngoài tại đỉnh A của ΔABC là ^A1=180o−ˆA=180o−120o=60o
Câu 2: Phương pháp: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông. Lời giải: Gọi độ dài cạnh huyền cần tìm là a(dm). Áp dụng định lí Pytago ta có: a2=22+22=8⇒a=√8dm Chọn B. Câu 3: Phương pháp: - Định lí tổng ba góc của một tam giác bằng 180o. - Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. Lời giải:
Theo định lí tổng ba góc của một tam giác ta có: ˆA+ˆB+ˆC=180oˆD+ˆM+ˆN=180o Mà ˆB=ˆM=90o;ˆA=ˆD (giả thiết) nên ˆC=ˆN Nếu có thêm điều kiện BC=MN. Xét hai tam giác vuông ABC và DMN có: ˆB=ˆM=90o ˆC=ˆN (chứng minh trên) BC=MN(điều kiện thêm) ⇒ΔABC=ΔDMN (cạnh góc vuông – góc nhọn kề). Chọn B.
Câu 4: Phương pháp: Sử dụng lí thuyết tam giác cân. Lời giải: Có hai cách chứng minh một tam giác là tam giác cân: - Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân. - Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân. Câu 5: Phương pháp: - Định lí tổng ba góc của một tam giác bằng 180o. - Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau. - Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và góc kề của tam giác kìa thì hai tam giác đó bằng nhau. - Hai góc đối đỉnh thì bằng nhau. Lời giải:
a) Xét ΔABC và ΔADE có: AB=AD (giả thiết) AC=AE (giả thiết) ^BAC=^DAE (đối đỉnh) ⇒ΔABC=ΔADE (c.g.c) ⇒BC=DE (hai cạnh tương ứng). b) Từ ΔABC=ΔADE (câu a) suy ra ^ABC=^ADE (hai góc tương ứng) (1) Mặt khác: ^ABC+^ABI=180o (hai góc kề bù) (2) ^ADE+^ADI=180o (hai góc kề bù) (3) Từ (1), (2) và (3) suy ra ^ABI=^ADI (điều phải chứng minh). c) Ta có AB=AD (giả thiết) AC=AE (giả thiết) Suy ra AB+AE=AD+AC hay BE=DC. Từ ΔABC=ΔADE (câu a) suy ra ˆC=ˆE (hai góc tương ứng). ^ABI=^ADI (câu b) hay ^EBI=^CDI Xét ΔIBE và ΔIDC ˆC=ˆE (chứng minh trên) ^EBI=^CDI (chứng minh trên) BE=DC (chứng minh trên) ⇒ΔIBE=ΔIDC (g.c.g) ⇒IB=ID (hai cạnh tương ứng). Chú ý: Sửa đề khác vở bài tập để bài toán có lời giải. HocTot.Nam.Name.Vn
|