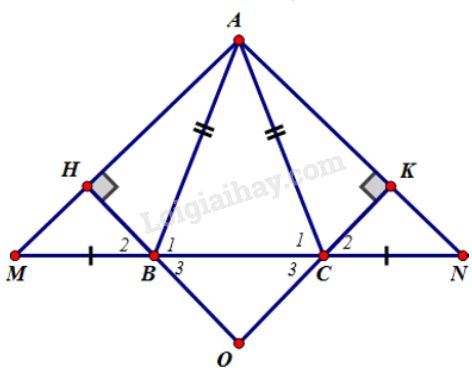
Bài 46 trang 141 Vở bài tập toán 7 tập 1Giải bài 46 trang 141 vở bài tập toán 7 tập 1. Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN. Đề bài Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM=CN. a) Chứng minh rằng tam giác AMN là tam giác cân. b) Kẻ BH⊥AM (H∈AM), kẻ CK⊥AN(K∈AN). Chứng minh rằng BH=CK. c) Chứng minh rằng AH=AK. d) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao? e) Khi ^BAC=60o và BM=CN=BC, hãy tính số đo các góc của tam giác AMN và xác định dạng của tam giác OBC. Phương pháp giải - Xem chi tiết - Chứng minh một tam giác là tam giác cân bằng cách chứng minh hai góc ở đáy bằng nhau. - Chứng minh các đoạn thẳng bằng nhau bằng cách chứng minh các tam giác bằng nhau. - Chứng minh tam giác là đều bằng cách chứng minh tam giác cân có một góc bằng 60o. Lời giải chi tiết
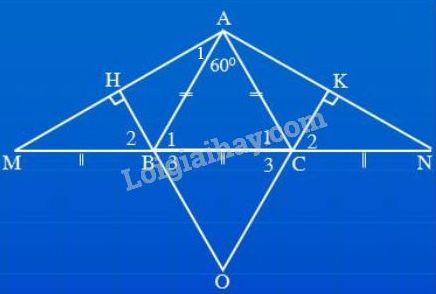
a) ∆ABC cân tại A, ⇒^B1=^C1 (góc đáy của tam giác cân). ⇒^ABM=^ACN (cùng bù với hai góc bằng nhau ^B1=^C1) ∆ABM và ∆ACN có: AB=AC (vì ∆ABC cân tại A) ^ABM=^ACN (chứng minh trên) BM=CN (gt) Do đó ∆ABM=∆ACN (c.g.c) suy ra ˆM=ˆN (hai góc tương ứng) Tam giác AMN có ˆM=ˆN nên là tam giác cân. b) Các tam giác vuông BHM và CKN có : cạnh huyền BM=CN (gt) góc nhọn ˆM=ˆN (chứng minh trên) Do đó ∆BHM=∆CKN (cạnh huyền - góc nhọn) suy ra BH=CK (hai cạnh tương ứng) c) Các tam giác vuông ABH và ACK có: cạnh huyền AB=AC (vì ∆ABC cân tại A) cạnh góc vuông BH=CK (chứng minh câu b) Do đó ΔABH=ΔACK suy ra AH=AK (hai cạnh tương ứng). d) ∆BHM=∆CKN (câu b) suy ra ^B2=^C2 (hai góc tương ứng) Ta lại có ^B3=^B2 (đối đỉnh); ^C3=^C2 (đối đỉnh) nên ^B3=^C3. Tam giác OBC có ^B3=^C3 nên là tam giác cân tại O. e) (h75) Ta có thêm ^BAC=60o và BM=CN=BC.
ΔABC cân có ˆA=60o nên là tam giác đều suy ra ^B1=^C1=^BAC=60o. Tam giác ABM có AB=BM (cùng bằng BC) nên là tam giác cân, suy ra ˆM=^BAM Ta lại có ˆM+^A1=^B1=60o nên ˆM=^A1=60o:2=30o Chứng minh tương tự, ta được: ˆN=30o Tam giác AMN có ˆM=ˆN=30o nên ^MAN=180o−30o−30o=120o Tam giác BHM vuông tại H có ˆM=30o nên ^B2=90o−30o=60o ^B3=^B2=60o Tam giác OBC cân (câu d) có ^B3=60o nên tam giác OBC là tam giác đều. HocTot.Nam.Name.Vn
|