Giải câu hỏi trắc nghiệm trang 112, 113 vở thực hành Toán 9

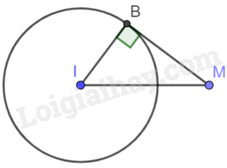
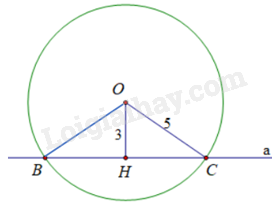
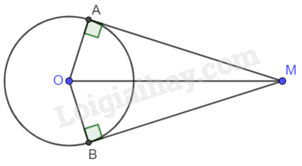
Câu 1

Trả lời Câu 1 trang 112 Vở thực hành Toán 9

Cho đường thẳng a và một điểm O cách a một khoảng bằng 6cm. Khẳng định nào sau đây là đúng về vị trí tương đối của đường thẳng a và đường tròn (O; 9cm)?

A. Đường thẳng a cắt đường tròn (O) tại hai điểm.

B. Đường thẳng a tiếp xúc với đường tròn (O).

C. Đường thẳng a và đường tròn (O) không có điểm chung.

D. Đường thẳng a và đường tròn (O) có duy nhất điểm chung.

Phương pháp giải:

Cho đường thẳng a và đường tròn (O; R). Gọi d là khoảng cách từ O đến a. Khi đó:

+ Đường thẳng a và đường tròn (O; R) cắt nhau khi $d < R$.

+ Đường thẳng a và đường tròn (O; R) tiếp xúc với nhau khi $d = R$.

+ Đường thẳng a và đường tròn (O; R) không giao nhau khi $d > R$.

Lời giải chi tiết:

Vì $6cm < 9cm$ nên đường thẳng a cắt đường tròn (O) tại hai điểm.

Chọn A

Câu 2

Trả lời Câu 2 trang 112 Vở thực hành Toán 9

Cho một điểm M nằm ngoài đường tròn (I; 6cm), vẽ tiếp tuyến MB đến đường tròn đó (B là tiếp điểm). Nếu $MI = 10cm$ thì độ dài MB bằng

A. 6 cm.

B. 8 cm.

C. 7 cm.

D. 10 cm.

Phương pháp giải:

+ Chứng minh tam giác MBI vuông tại B.

+ Áp dụng định lí Pythagore vào tam giác MBI vuông tại B ta tính được MB.

Lời giải chi tiết:

Vì MB là tiếp tuyến của (I) nên $MB \bot IB$ tại B. Khi đó tam giác IMB vuông tại B.

Áp dụng định lí Pythagore vào tam giác MBI vuông tại B ta có:

$I{B^2} + M{B^2} = M{I^2}$

$MB = \sqrt {M{I^2} - I{B^2}}  = \sqrt {{{10}^2} - {6^2}}  = 8\left( {cm} \right)$

Chọn B

Câu 3

Trả lời Câu 3 trang 112 Vở thực hành Toán 9

Cho đường thẳng a và một điểm O cách a là 3cm. Vẽ đường tròn (O; 5cm). Gọi B, C là các giao điểm của đường thẳng a và (O). Diện tích của tam giác OBC bằng

A. $10c{m^2}$.

B. $6c{m^2}$.

C. $24c{m^2}$.

D. $12c{m^2}$.

Phương pháp giải:

+ Qua O kẻ đường thẳng vuông góc với BC tại H. Khi đó, OH là khoảng cách từ O đến đường thẳng a. Do đó, $OH = 3cm$.

+ Chứng minh tam giác OBC cân tại O, suy ra OH là đường trung tuyến, suy ra $BH = HC = \frac{1}{2}BC$.

+ Áp dụng định lí Pythagore vào tam giác BOH vuông tại H tính được BH, từ đó tính được BC.

+ Diện tích tam giác OBC là: $S = \frac{1}{2}OH.BC$

Lời giải chi tiết:

Qua O kẻ đường thẳng vuông góc với BC tại H. Khi đó, OH là khoảng cách từ O đến đường thẳng a. Do đó, $OH = 3cm$.

Tam giác OBC có: $OB = OC$ (bán kính (O)) nên tam giác BOC cân tại O. Do đó, OH là đường cao đồng thời là đường trung tuyến của tam giác OBC. Suy ra $BH = HC = \frac{1}{2}BC$.

Áp dụng định lí Pythagore vào tam giác BOH vuông tại H có:

$O{H^2} + B{H^2} = O{B^2}$ nên $BH = \sqrt {B{O^2} - O{H^2}}  = \sqrt {{5^2} - {3^2}}  = 4\left( {cm} \right)$ nên $BC = 2BH = 2.4 = 8\left( {cm} \right)$

Diện tích tam giác OBC là: $S = \frac{1}{2}OH.BC = \frac{1}{2}.3.8 = 12\left( {c{m^2}} \right)$

Chọn D

Câu 4

Trả lời Câu 4 trang 113 Vở thực hành Toán 9

Cho đường tròn (O) và điểm M nằm ngoài đường tròn, vẽ hai tiếp tuyến MA và MB của đường tròn (O). Biết $\widehat {AMB} = {35^o}$. Số đo cung nhỏ AB là

A. ${145^o}$.

B. ${215^o}$.

C. ${125^o}$.

D. ${235^o}$.

Phương pháp giải:

+ Chứng minh $\widehat {MAO} = \widehat {MBO} = {90^o}$.

+ Tứ giác $\widehat {MAO} + \widehat {MBO} + \widehat {AMB} + \widehat {AOB} = {360^o}$, từ đó tính được góc AOB, suy ra số đo cung nhỏ AB.

Lời giải chi tiết:

Vì MA, MB là tiếp tuyến của đường tròn (O) nên $MA \bot OA,MB \bot OB$ nên $\widehat {MAO} = \widehat {MBO} = {90^o}$.

Tứ giác MBOA có: $\widehat {MAO} + \widehat {MBO} + \widehat {AMB} + \widehat {AOB} = {360^o}$

$\widehat {AOB} = {360^o} - \widehat {MAO} - \widehat {MBO} - \widehat {AMB} = {360^o} - {90^o} - {90^o} - {35^o} = {145^o}$

Vì góc ở tâm AOB chắn cung nhỏ AB nên số đo cung nhỏ AB bằng ${145^o}$.

Chọn A