Giải câu hỏi trắc nghiệm trang 101 vở thực hành Toán 9Cho đường tròn (O) có bán kính bằng 12cm. Khi đó, dây lớn nhất của đường tròn (O; 12cm) có độ dài bằng A. 6cm. B. 36cm. C. 12cm. D. 24cm. Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Lựa chọn câu để xem lời giải nhanh hơn
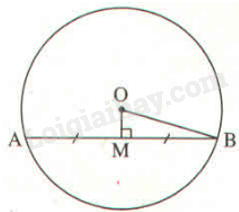
Chọn phương án đúng cho mỗi câu sau: Câu 1 Trả lời Câu 1 trang 101 Vở thực hành Toán 9 Cho đường tròn (O) có bán kính bằng 12cm. Khi đó, dây lớn nhất của đường tròn (O; 12cm) có độ dài bằng A. 6cm. B. 36cm. C. 12cm. D. 24cm. Phương pháp giải: Trong một đường tròn, đường kính là dây lớn nhất. Lời giải chi tiết: Dây lớn nhất của đường tròn (O; 12cm) là đường kính nên dây lớn nhất có độ dài là: 2.12=24(cm) Chọn D Câu 2 Trả lời Câu 2 trang 101 Vở thực hành Toán 9 Cho đường tròn (O; R) và điểm M nằm trong đường tròn (O). Kẻ dây AB của đường tròn (O) nhận M làm trung điểm. Biết \(R = 5cm\) và \(OM = 1,4cm\). Độ dài dây AB là A. 9,5cm. B. 9,6cm. C. 9,8cm. D. 9cm. Phương pháp giải: + Chứng minh tam giác AOB cân tại O, suy ra OM là đường trung tuyến đồng thời là đường cao. + Áp dụng định lí Pythagore vào tam giác OMB vuông tại M ta tính được MB. + \(AB = 2MB\). Lời giải chi tiết:
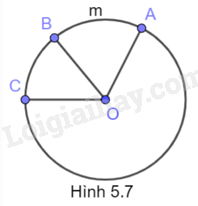
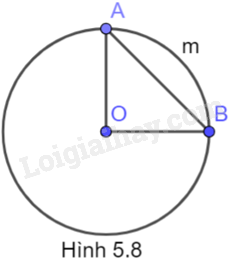
Tam giác AOB có \(OA = OB\) (bán kính (O)) nên tam giác AOB cân tại O. Do đó, OM là đường trung tuyến đồng thời là đường cao. Áp dụng định lí Pythagore vào tam giác OMB vuông tại M có: \(M{B^2} + O{M^2} = O{B^2}\) Suy ra \(MB = \sqrt {O{B^2} - O{M^2}} = \sqrt {{5^2} - {{1,4}^2}} = 4,8\left( {cm} \right)\) Do đó, \(AB = 2MB = 2.4,8 = 9,6\left( {cm} \right)\) Chọn B Câu 3 Trả lời Câu 3 trang 101 Vở thực hành Toán 9 Cho Hình 5.7. Khẳng định nào sau đây là đúng? A. Cung AmB bị chắn bởi góc ở tâm AOB. B. Góc ở tâm AOC chắn cung AB. C. Cung AmB bị chắn bởi góc ở tâm BOC. D. Góc ở tâm AOC chắn cung BC. Phương pháp giải: Quan sát hình và rút ra kết luận. Lời giải chi tiết: Cung AmB bị chắn bởi góc ở tâm AOB. Chọn A Câu 4 Trả lời Câu 4 trang 101 Vở thực hành Toán 9 Cho đường tròn (O; R), vẽ dây \(AB = \sqrt 2 R\) (H.5.8). Số đo của cung AmB là A. \({45^o}\). B. \({90^o}\). C. \({270^o}\). D. \({60^o}\). Phương pháp giải: Trong một đường tròn, số đo cung nhỏ bằng số đo của góc ở tâm chắn cung đó. Lời giải chi tiết: Vì A, B thuộc (O) nên \(OA = OB = R\) Ta có: \(A{B^2} = O{A^2} + O{B^2}\) nên tam giác OAB vuông tại O. Do đó, \(\widehat {AOB} = {90^o}\) Vì góc ở tâm AOB chắn cung AmB nên \(sđ\overset\frown{AmB}=\widehat{AOB}={{90}^{o}}\) Chọn B
|