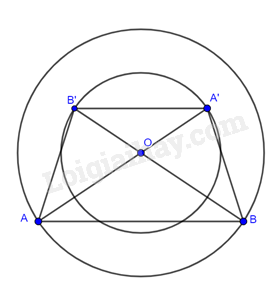
Giải bài tập 7 trang 100 SGK Toán 9 tập 1 - Cánh diềuCho hai đường tròn cùng tâm (left( {O;R} right),left( {O;r} right)) với (R > r). Các điểm (A,B) thuộc đường tròn (left( {O;R} right)), các điểm (A',B') thuộc đường tròn (left( {O;r} right)) sao cho (O,A,A') thẳng hàng; (O,B,B') thẳng hàng và điểm (O) không thuộc đường thẳng (AB). Chứng minh: a) (frac{{OA'}}{{OA}} = frac{{OB'}}{{OB}}). b) (AB//A'B'). Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Cho hai đường tròn cùng tâm (O;R),(O;r)(O;R),(O;r) với R>rR>r. Các điểm A,BA,B thuộc đường tròn (O;R)(O;R), các điểm A′,B′ thuộc đường tròn (O;r) sao cho O,A,A′ thẳng hàng; O,B,B′ thẳng hàng và điểm O không thuộc đường thẳng AB. Chứng minh: a) OA′OA=OB′OB. b) AB//A′B′. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Dựa vào các kiến thức đã học để giải bài toán. Lời giải chi tiết
a) Do các điểm A,B thuộc đường tròn (O;R) nên OA=OB=R. Do các điểm A′,B′ thuộc đường tròn (O;r) nên OA′=OB′=r. Ta có: OA′OA=rR;OB′OB=rR. Vậy OA′OA=OB′OB. b) Xét tam giác OAB có: OA′OA=OB′OB Nên AB//A′B′ (Định lí Thalet đảo).
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|