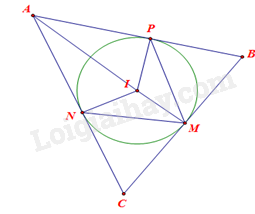
Giải bài tập 2 trang 79 SGK Toán 9 tập 2 - Cánh diều

Đề bài

Cho đường tròn (I) nội tiếp tam giác ABC và lần lượt tiếp xúc với các cạnh BC, CA, AB tại M, N, P. Chứng minh $\widehat {AIN} = \widehat {PMN} = \frac{1}{2}\widehat {PIN.}$

Lời giải chi tiết

Xét (I) có:

$\widehat {PIN}$ là góc ở tâm chắc cung NP nên $\widehat {PIN}$= sđ$\overset\frown{NP}$.

$\widehat {PMN}$ là góc nội tiếp chắc cung NP nên $\widehat {PMN}$ = $\frac{1}{2}$sđ$\overset\frown{NP}$.

Suy ra $\widehat {PMN} = \frac{1}{2}\widehat {PIN.}$(1)

Ta lại có: $IN \bot AC,IP \bot AB$ nên AB, AC là 2 tiếp tuyến của (I) nên IA là tia phân giác của góc PIN, hay $\widehat {AIN} = \frac{1}{2}\widehat {PIN.}$(2)

Từ (1) và (2) ta có $\widehat {AIN} = \widehat {PMN} = \frac{1}{2}\widehat {PIN.}$