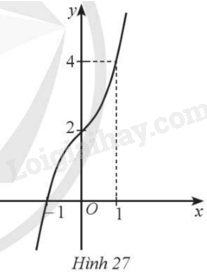
Giải bài 96 trang 41 sách bài tập toán 12 - Cánh diềuĐường cong ở Hình 27 là đồ thị của hàm số: A. \(y = 2{{\rm{x}}^3} + 2\). B. \(y = {x^3} - {x^2} + 2\). C. \(y = - {x^3} + 3{\rm{x}} + 2\). D. \(y = {x^3} + x + 2\). Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa Đề bài Đường cong ở Hình 27 là đồ thị của hàm số: A. \(y = 2{{\rm{x}}^3} + 2\). B. \(y = {x^3} - {x^2} + 2\). C. \(y = - {x^3} + 3{\rm{x}} + 2\). D. \(y = {x^3} + x + 2\).
Phương pháp giải - Xem chi tiết ‒ Dựa vào hình dáng của đồ thị hàm số. ‒ Xét các điểm trên đồ thị hàm số. Lời giải chi tiết Dựa vào hình dáng của đồ thị hàm số ta có: \(a > 0\) và \(y' > 0\) nên loại A, C. Đồ thị hàm số đi qua điểm \(\left( { - 1;0} \right)\) nên loại B. Chọn D.
|