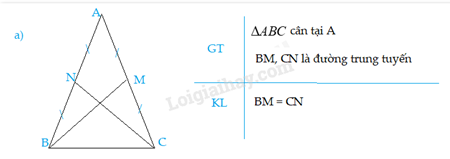
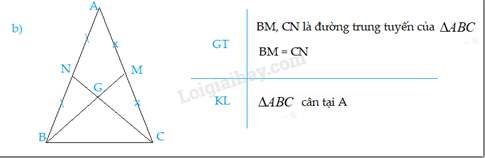
Giải bài 9.21 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức

Đề bài

Chứng minh rằng:

a) Trong một tam giác cân, hai đường trung tuyến ứng với 2 cạnh bên là hai đoạn thẳng bằng nhau.

b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Lời giải chi tiết

a) 

Gọi BM, CN là 2 đường trung tuyến của $\Delta ABC$

$\Rightarrow$MA = MC = $\dfrac{1}{2}$AC; NA = NB = $\dfrac{1}{2}$AB

Vì $\Delta ABC$ cân tại A nên AB = AC ( tính chất)

Do đó, AM = MC = NA = NB

Xét $\Delta$ANC và $\Delta$AMB, ta có:

AN = AM

$\widehat A$ chung

AC = AB

$\Rightarrow$$\Delta$ANC = $\Delta$AMB (c.g.c)

$\Rightarrow$ NC = MB ( 2 cạnh tương ứng)

Vậy 2 đường trung tuyến ứng với 2 cạnh bên của tam giác cân là hai đoạn thẳng bằng nhau.

b) 

Vì $∆ABC$ có hai đường trung tuyến $BM$ và $CN$ cắt nhau ở $G$

$\Rightarrow$ $G$ là trọng tâm của tam giác $ABC$.

$\Rightarrow  GB = \dfrac{2}{3}BM$; $GC = \dfrac{2}{3}CN$ ( tính chất đường trung tuyến trong tam giác)

Mà $BM = CN$ (giả thiết) nên $GB = GC.$

Tam giác $GBC$ có $GB = GC$ nên $∆GBC$ cân tại $G$.

$\Rightarrow$ $\widehat{GCB} = \widehat{GBC}$ (Tính chất tam giác cân).

Xét $∆BCN$ và $∆CBM$ có: 

+) $BC$ là cạnh chung

+) $CN = BM$ (giả thiết)

+) $\widehat{GCB} = \widehat{GBC}$ (chứng minh trên)

Suy ra $∆BCN = ∆CBM$ (c.g.c)

 $\Rightarrow$ $\widehat{NBC} = \widehat{MCB}$ (hai góc tương ứng).

$\Rightarrow ∆ABC$ cân tại $A$ (tam giác có hai góc bằng nhau là tam giác cân)

Vậy tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.