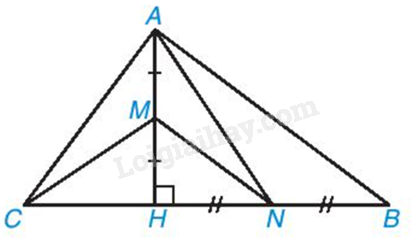
Giải bài 9 trang 106 vở thực hành Toán 8 tập 2Cho tam giác ABC có đường cao AH. Biết AH = 12cm, CH = 9cm, BH = 16cm. Lấy M, N lần lượt là trung điểm của AH, BH Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên Đề bài Cho tam giác ABC có đường cao AH. Biết AH = 12cm, CH = 9cm, BH = 16cm. Lấy M, N lần lượt là trung điểm của AH, BH a) Chứng minh rằng ABC là tam giác vuông tại A b) Chứng minh rằng MN ⊥ AC và CM ⊥ AN c) Tính diện tích tam giác AMN
Phương pháp giải - Xem chi tiết Áp dụng định lí Pythagore, Pythagore đảo. Lời giải chi tiết a) Áp dụng định lí Pythagore cho tam giác AHC vuông tại H, ta có: AC2 = AH2 + CH2 = 225, hay AC = 15 cm. Áp dụng định lí Pythagore cho tam giác AHB vuông tại H, ta có: AB2 = AH2 + BH2 = 400, hay AB = 20 cm. Mặt khác BC = BH + CH = 25 cm. Do đó BC2 = AB2 + AC2. Vì vậy, theo định lí Pythagore đảo thì tam giác ABC vuông tại A. b) Do MN // AB và AB ⊥ AC nên MN ⊥ AC. ΔACN có: AH ⊥ CN (theo giả thiết), MN ⊥ AC (chứng minh trên). Vậy M là trực tâm của ΔACN, do đó CM ⊥ AN. c) Ta có SAMN=AM.HN2=AH.HB8=24(cm2).
|