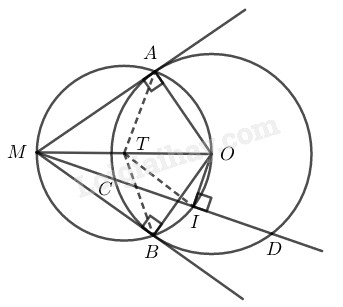
Bài 8.2 phần bài tập bổ sung trang 109 SBT toán 9 tập 2Giải bài 8.2 phần bài tập bổ sung trang 109 sách bài tập toán 9. Cho đường tròn tâm O bán kính R và điểm M ở ngoài đường tròn đó... Đề bài Cho đường tròn tâm \(O\) bán kính \(R\) và điểm \(M\) ở ngoài đường tròn đó. Qua điểm \(M\) kẻ hai tiếp tuyến \(MA,\) \(MB\) với đường tròn \((O).\) Qua điểm \(M\) kẻ cát tuyến \(MCD\) với đường tròn \((O)\) (tức là đường thẳng đi qua điểm \(M\) và cắt đường tròn tại hai điểm \(C, D).\) Gọi \(I\) là trung điểm của dây \(CD.\) Khi đó \(MAOIB\) có là ngũ giác nội tiếp hay không\(?\) Phương pháp giải - Xem chi tiết Ta sử dụng kiến thức: +) Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy. +) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm. +) Nếu các đỉnh của đa giác cùng nhìn một cạnh dưới góc vuông thì đa giác đó nội tiếp đường tròn. Lời giải chi tiết
Khi cát tuyến \(MCD\) không đi qua \(O.\) Xét đường tròn \((O)\) có: \(IC = ID\;\; (gt)\) \( \Rightarrow \) \(OI ⊥ CD\) (đường kính đi qua điểm chính giữa của dây không đi qua tâm thì vuông góc với dây đó) \( \Rightarrow \widehat {MIO} = 90^\circ \) \(MA ⊥ OA\) (tính chất tiếp tuyến) \( \Rightarrow \widehat {MAO} = 90^\circ \) \(MB ⊥ OB\) (tính chất tiếp tuyến) \( \Rightarrow \widehat {MBO} = 90^\circ \) \(A, I, B\) nhìn \(MO\) dưới một góc bằng \(90^\circ\) nên \(A, I, B\) nằm trên đường tròn đường kính \(MO.\) Vậy: Ngũ giác \(MAOIB\) nội tiếp. (Khi cát tuyến \(MCD\) đi qua \(O\) ngũ giác \(MAOIB\) suy biến thành tứ giác \(MAOB\) chứng minh tương tự). HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
