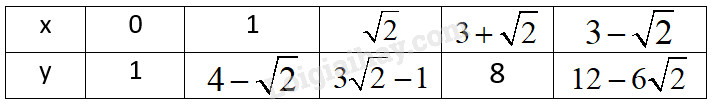Bài 8 trang 62 SBT toán 9 tập 1

LG câu a

Hàm số là đồng biến hay nghịch biến trên \(R\)? vì sao?

Phương pháp giải:

Hàm số bậc nhất là hàm số được cho bởi công thức \(y = ax + b\), trong đó \(a,b\) là các số cho trước và \(a \ne 0\).

Hàm số bậc nhất \(y = ax + b\) xác định với mọi giá trị của x thuộc R và có tính chất sau:

a) Đồng biến trên \(R\), khi \(a > 0\).

b) Nghịch biến trên \(R\), khi \(a < 0\).

Lời giải chi tiết:

Hàm số \(y = \left( {3 - \sqrt 2 } \right)x + 1\) có hệ số \(a = 3 - \sqrt 2 \), hệ số \(b = 1\) .

Ta có: \(3 - \sqrt 2  > 0\) nên hàm số đồng biến trên \(R\)

LG câu b

Tính các giá trị tương ứng của \(y\) khi \(x\) nhận các giá trị sau: 

\(0;\)   \(1;\)    \(\sqrt 2 \);  \(3 + \sqrt 2 \);  \(3 - \sqrt 2 \).

Phương pháp giải:

Thay các giá trị của \(x\) vào hàm số \(y = \left( {3 - \sqrt 2} \right)x + 1\) để tìm \(y\) tương ứng. 

Lời giải chi tiết:

Các giá trị của \(y\) được thể hiện trong bảng sau:

LG câu c

Tính các giá trị tương ứng của \(x\) khi \(y\) nhận các giá trị sau:

\(0;\)   \(1;\)   \(8;\)   \(2 + \sqrt 2 \);  \(2 - \sqrt 2 \). 

Phương pháp giải:

Thay các giá trị của \(y\) vào hàm số \(y = \left( {3 - \sqrt 2} \right)x + 1\) để tìm \(x\) tương ứng. 

Lời giải chi tiết:

Các giá trị tương ứng của \(x\): 

+) Với  \(y = 0\) 

\(\eqalign{
& y = 0 \Leftrightarrow \left( {3 - \sqrt 2 } \right)x + 1 = 0 \cr 
& \Leftrightarrow \left( {3 - \sqrt 2 } \right)x = - 1 \cr 
& \Leftrightarrow x = {{ - 1} \over {3 - \sqrt 2 }} \cr 
& \Leftrightarrow x = {{ - 1\left( {3 + \sqrt 2 } \right)} \over {\left( {3 - \sqrt 2 } \right)\left( {3 + \sqrt 2 } \right)}} \cr 
& \Leftrightarrow x = {{ - \left( {3 + \sqrt 2 } \right)} \over 7} \cr} \)

+) Với \(y = 1\)

\(\eqalign{
& y = 1 \Leftrightarrow \left( {3 - \sqrt 2 } \right)x + 1 = 1 \cr 
& \Leftrightarrow \left( {3 - \sqrt 2 } \right)x = 0 \cr 
& \Leftrightarrow x = 0 \cr} \)

+) Với \(y = 8\)

\(\eqalign{
& y = 8 \Leftrightarrow \left( {3 - \sqrt 2 } \right)x + 1 = 8 \cr 
& \Leftrightarrow \left( {3 - \sqrt 2 } \right)x = 7 \cr 
& \Leftrightarrow x = {7 \over {3 - \sqrt 2 }} \cr 
& \Leftrightarrow x = {{7\left( {3 + \sqrt 2 } \right)} \over {\left( {3 - \sqrt 2 } \right)\left( {3 + \sqrt 2 } \right)}} \cr 
& \Leftrightarrow x = {{7\left( {3 + \sqrt 2 } \right)} \over 7} = 3 + \sqrt 2 \cr} \)

+) Với \(y = 2 + \sqrt 2 \)

\(\eqalign{
& \Leftrightarrow \left( {3 - \sqrt 2 } \right)x + 1 = 2 + \sqrt 2 \cr 
& \Leftrightarrow \left( {3 - \sqrt 2 } \right)x = 1 + \sqrt 2 \cr 
& \Leftrightarrow x = {{1 + \sqrt 2 } \over {3 - \sqrt 2 }}\cr  &= {{\left( {1 + \sqrt 2 } \right)\left( {3 + \sqrt 2 } \right)} \over {\left( {3 - \sqrt 2 } \right)\left( {3 + \sqrt 2 } \right)}} \cr 
& = {{3 + \sqrt 2 + 3\sqrt 2 + 2} \over {9 - 2}} = {{5 + 4\sqrt 2 } \over 7} \cr} \)

+) Với \(y = 2 - \sqrt 2 \)

\(\eqalign{
& \Leftrightarrow \left( {3 - \sqrt 2 } \right)x + 1 = 2 - \sqrt 2 \cr 
& \Leftrightarrow \left( {3 - \sqrt 2 } \right)x = 1 - \sqrt 2 \cr 
& \Leftrightarrow x = {{1 - \sqrt 2 } \over {3 - \sqrt 2 }}\cr & = {{\left( {1 - \sqrt 2 } \right)\left( {3 + \sqrt 2 } \right)} \over {\left( {3 - \sqrt 2 } \right)\left( {3 + \sqrt 2 } \right)}} \cr 
& = {{3 + \sqrt 2 - 3\sqrt 2 - 2} \over {9 - 2}} = {{1 - 2\sqrt 2 } \over 7} \cr} \)

HocTot.Nam.Name.Vn