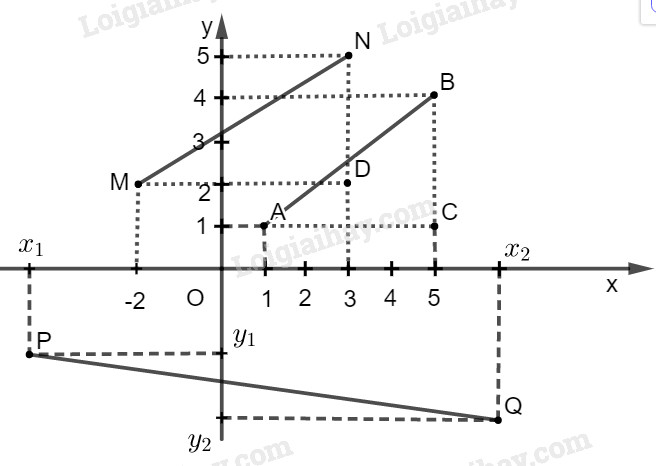
Bài 13 trang 63 SBT toán 9 tập 1

Đề bài

Tìm khoảng cách giữa hai điểm trên mặt phẳng tọa độ , biết rằng :

a) A(1;1), B(5;4);  

b) M(-2;2), N(3;5);

c) P(\(x_1; y_1\) ), Q(\(x_2; y_2\) )

Lời giải chi tiết

a) Lấy thêm điểm \(C(5;1)\) như hình vẽ.

Ta có :

Áp dụng Pytago vào tam giác ABC ta có:

\(\eqalign{
& A{B^2} = A{C^2} + B{C^2} \cr 
& = {\left( {5 - 1} \right)^2} + {\left( {4 - 1} \right)^2} \cr 
& = 16 + 9 = 25 \cr} \)

\(AB = \sqrt {25}  = 5\) 

Cách 2: \(AB = \sqrt {{{\left( {{5} - {1}} \right)}^2} + {{\left( {{4} - {1}} \right)}^2}} \) = \(\sqrt {25}  = 5\) 

b) Lấy thêm điểm \(D(3;2)\) như hình vẽ.

Ta có :

Áp dụng Pytago vào tam giác MND ta có:

\(\eqalign{
& M{N^2} = M{D^2} + N{D^2} \cr 
& = {\left( {3 + 2} \right)^2} + {\left( {5 -2} \right)^2} \cr 
& = 25 + 9 = 34 \cr} \)

\(MN = \sqrt {34}  \approx 5,83\)  

Cách 2: \(CD = \sqrt {{{\left( {{3} - {-2}} \right)}^2} + {{\left( {{5} - {2}} \right)}^2}} \) = \(\sqrt {34}\approx 5,83\) 

c) Ta có :

\(PQ = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \)

HocTot.Nam.Name.Vn