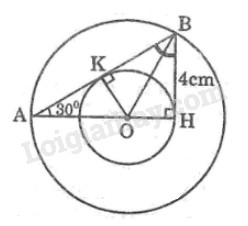
Bài 78 trang 114 SBT toán 9 tập 2

Đề bài

Cho tam giác \(AHB\) có \(\widehat H = 90^\circ ,\widehat A = 30^\circ \) và \(BH = 4cm.\) Tia phân giác của góc \(B\) cắt \(AH\) tại \(O.\) Vẽ đường tròn \((O; OH)\) và đường tròn \((O; OA).\)

\(a)\) Chứng minh đường tròn \((O; OH)\) tiếp xúc với cạnh \(AB.\)

\(b)\) Tính diện tích hình vành khăn nằm giữa hai đường tròn trên.

Lời giải chi tiết

\(a)\) Kẻ \(OK \bot AB\) tại \(K\) 

Vì \(BO\) là đường phân giác của \(\widehat B\) (gt)

\( \Rightarrow OK = OH\) (tính chất đường phân giác)

Suy ra: \(OK\) cũng là bán kính của đường tròn \((O;OH)\)

Vậy đường tròn \((O; OH)\) tiếp xúc với \(AB\) tại \(K.\) 

\(b)\) \(\Delta AHB\) có \(\widehat H = {90^0}\); \(\widehat A = {30^0}\)

Suy ra: \(\widehat B = {60^0} \Rightarrow \widehat {ABO} =\displaystyle {1 \over 2}\widehat B = {30^0}\)

Suy ra: \(∆OAB\) cân tại \(O\) nên \(OB = OA\)

Vậy \(B \in (O; OA)\)

\(∆BHO\) có \(\widehat H = {90^0}\); \(\widehat {OBH} = {30^0}\)

\(OH = BH.\tan {30^0} \)\(=\displaystyle  4.{{\sqrt 3 } \over 3} = {{4\sqrt 3 } \over 3}\;\;(cm)\)

\(OB = \displaystyle {{BH} \over {\cos \widehat {OBH}}} \)\(= \displaystyle {4 \over {\cos {{30}^0}}} = {4 \over \displaystyle {{{\sqrt 3 } \over 2}}} = {{8\sqrt 3 } \over 3}\) \((cm)\)

Diện tích đường tròn nhỏ: \(S_1=\displaystyle \pi {\left( {{{4\sqrt 3 } \over 3}} \right)^2} = {{16\pi } \over 3}\)  \((cm^2)\)

Diện tích đường tròn lớn: \({S_2} = \displaystyle \pi {\left( {{{8\sqrt 3 } \over 3}} \right)^2} = {{64\pi } \over 3}\) \((cm^2)\)

Diện tích hình vành khăn:

\(S={S_2} - {S_1} = \displaystyle {{64\pi } \over 3} - {{16\pi } \over 3} \)\(=\displaystyle  {{48\pi } \over 3} = 16\pi \) \((cm^2)\)

HocTot.Nam.Name.Vn