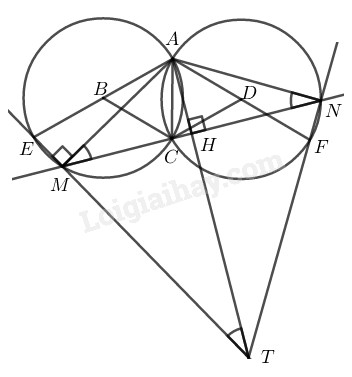
Bài 3.1 phần bài tập bổ sung trang 114 SBT toán 9 tập 2

Đề bài

Cho tam giác đều \(ACB\) và \(ACD,\) cạnh \(a.\) Lần lượt lấy \(B\) và \(D\) làm tâm vẽ hai đường tròn bán kính \(a.\) Kẻ các đường kính \(ABE\) và \(ADF.\) Trên cung nhỏ \(CE\) của đường tròn tâm \(B\) lấy điểm \(M\) (không trùng với \(E\) và \(C\)). Đường thẳng \(CM\) cắt đường tròn tâm \(D\) tại điểm thứ hai là \(N.\) Hai đường thẳng \(EM\) và \(NF\) cắt nhau tại điểm \(T.\) Gọi \(H\) là giao điểm của \(AT\) và \(MN.\) Chứng minh:

\(a)\) \(MNT\) là tam giác đều.

\(b)\) \(AT = 4AH.\)

Lời giải chi tiết

\(a)\) Trong đường tròn \((B)\) ta có: 

\(\widehat {AMC} = \displaystyle {1 \over 2}\widehat {ABC}\) (hệ quả góc nội tiếp) mà \(\widehat {ABC} = 60^\circ \) (vì \(∆ABC\) đều)

\( \Rightarrow \widehat {AMC} = 30^\circ \)

\(\widehat {AME} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn \((B)\))

\( \Rightarrow \widehat {AMT} = 90^\circ \)

\(\widehat {TMN} = \widehat {AMT} - \widehat {AMC}\)\( = 90^\circ  - 30^\circ  = 60^\circ \)

Trong đường tròn \((D)\) ta có:

\(\widehat {ANC} =\displaystyle{1 \over 2}\widehat {ADC}\) (Hệ quả góc nội tiếp) mà \(\widehat {ADC} = 60^\circ \) (vì \(∆ADC\) đều) \( \Rightarrow \widehat {ANC} = 30^\circ \)

\(\widehat {ANF} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn \((D)\))

\( \Rightarrow \widehat {ANC} + \widehat {CNF} = 90^\circ\)

\(  \Rightarrow \widehat {CNF} = 90^\circ  - \widehat {ANC}\)\( = 90^\circ  - 30^\circ  = 60^\circ \) hay \(\widehat {MNT} = 60^\circ \)

Vậy \(∆TMN\) đều.

\(b)\) \(\widehat {AMC} = \widehat {ANC} = 30^\circ \) (theo câu a)

\( \Rightarrow \Delta AMN\) cân tại \(A\) \( \Rightarrow  AM = AN\) nên \(A\) nằm trên đường trung trực \(MN\)

Vì \(∆TMN\) đều \( \Rightarrow TM = TN\) nên \(T\) nằm trên đường trung trực \(MN\)

Suy ra \(AT\) là đường trung trực của \(MN\) nên \(AT ⊥ MN\)

\(∆AHM\) có \(\widehat {AHM} = 90^\circ \)

\(AM =\displaystyle{{AH} \over {\sin M}} = {{AH} \over {\sin 30^\circ }}\)\( =\displaystyle {{AH} \over {\displaystyle{1 \over 2}}} = 2AH\)     \(         (1)\)

Vì  \(∆TMN\) đều có \(TH ⊥ MN\) nên \(TH\) cũng là đường phân giác của \(\widehat T\) nên \(\widehat {MTA} = 30^\circ \)

\(∆AMT\) có \(\widehat {AMT} = 90^\circ \)

\(AT = \displaystyle{{AM} \over {\sin \widehat {MTA}}} = {\displaystyle{AM} \over {\displaystyle{1 \over 2}}} = 2AM\)\(\;  (2)\)

Từ \((1)\) và \((2)\) suy ra: \(AT =2AM=2.2AH= 4AH\)

Vậy \(AT=4AH.\)

HocTot.Nam.Name.Vn