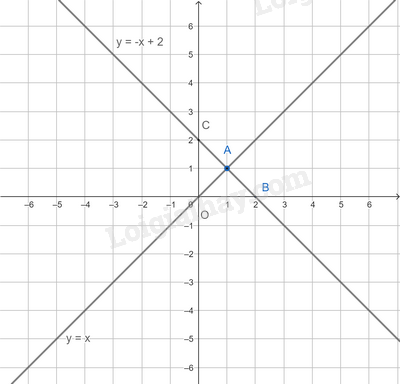
Giải bài 7.35 trang 54 SGK Toán 8 tập 2 - Kết nối tri thứcTrong mặt phẳng tọa độ Oxy, cho hai đường thẳng Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên Đề bài Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng y=x và y=−x+2 a) Vẽ hai đường thẳng đã cho trên cùng một mặt phẳng tọa độ b) Tìm giao điểm A của hai đường thẳng đã cho c) Gọi B là giao điểm của đường thẳng y=−x+2 và trục Ox. Chứng minh tam giác OAB vuông tại A, tức hai đường thẳng y=x và y=−x+2 vuông góc với nhau d) Có nhận xét gì về tích hai hệ số góc của hai đường thẳng đã cho Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Vẽ hai đường thẳng y = x và y = −x + 2 trên mặt phẳng tọa độ bằng cách xác định hai điểm thuộc mỗi đường thẳng. b) Quan sát đồ thị hàm số y = x và y = 0x + 2 xác định tọa độ điểm A là giao điểm của hai đường thẳng đã cho. c) Lấy C là giao điểm của đường thẳng y = -x + 2 và trục Oy, chứng minh tam giác OBC vuông cân tại O. Chứng minh AB = AC => \(OA \bot AB\) hay tam giác OAB vuông cân tại A. d) Xác định hệ số góc của hai đường thẳng đã cho và tính tích của chúng Lời giải chi tiết a) * Xét đường thẳng y = x Cho x = 1 suy ra y = 1 nên điểm (1; 1) thuộc đường thẳng y = x Đường thẳng y = x đi qua 2 điểm O(0; 0) và (1; 1)\ * Xét đường thẳng y = -x + 2 Cho x = 2 thì y = -2 + 2 = 0 nên điểm (2; 0) thuộc đường thẳng y = - x+ 2 Cho y = 2 suy ra x = 0 nên điểm (0; 2 ) thuộc đường thẳng y = -x + 2 Đường thẳng y = - x + 2 đi qua hai điểm (2; 0) và (0; 2) b) Gọi A(x0; y0) là giao điểm của hai đường thẳng đã cho. Khi đó, cả hai đường thẳng đã cho đồng thời đi qua điểm A, do đó, ta có: y0 = x0 và y0 = -x0 + 2, suy ra x0 = −x0 + 2, hay x0 = 1. Vậy hai đường thẳng đã cho cắt nhau tại điểm A(1;1). c) Giao điểm của đường thẳng y = -x + 2 và trục Ox là B(2; 0). Suy ra OB = 2. Vì OA là đường chéo của hình vuông có cạnh bằng 1 nên suy ra OA = \(\sqrt 2 \). Vì AB là đường chéo của hình vuông có cạnh bằng 1 nên suy ra AB = \(\sqrt 2 \). Ta có: \(O{A^2} + A{B^2} = {\left( {\sqrt 2 } \right)^2} + {\left( {\sqrt 2 } \right)^2} = 4;O{B^2} = 4.\) Do đó OA2 + AB2 = OB2, suy ra tam giác OAB vuông tại A (theo định lí Pythagore đảo). d) Đường thẳng y = x có hệ số góc bằng 1. Đường thẳng y = - x + 1 có hệ số góc bằng -1 Tích của hai hệ số góc bằng -1
|