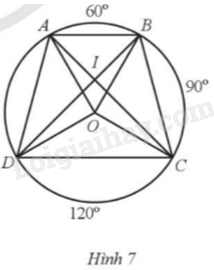
Giải bài 7 trang 85 sách bài tập toán 9 - Cánh diều tập 2

Đề bài

Trên đường tròn (O) bán kính R, lấy các điểm A, B, C, D sao cho \(sđ\overset\frown{AB}={{60}^{o}}\); \(sđ\overset\frown{BC}={{90}^{o}}\); \(sđ\overset\frown{CD}={{120}^{o}}\) (Hình 7).

a) Xác định tâm và tính theo R bán kính đường tròn ngoại tiếp của các tam giác OAB, OBC, OAD, OCD.

b) Gọi I là giao điểm của AC và BD. Tính bán kính đường tròn ngoại tiếp của các tam giác IAB, IBC, IAD, IDC.

 

Lời giải chi tiết

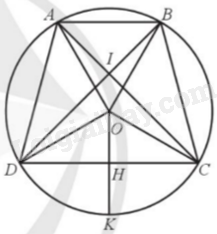
a) Gọi G là trọng tâm của tam giác OAB. Tam giác OAB là tam giác đều cạnh AB = R nên có tâm đường tròn ngoại tiếp là G và bán kính đường tròn ngoại tiếp là \(\frac{{R\sqrt 3 }}{3}\).

Tam giác OBC vuông tại O, có cạnh huyền BC = \(R\sqrt 2 \) nên tâm, bán kính của đường tròn ngoại tiếp của nó lần lượt là trung điểm E của BC và \(\frac{{R\sqrt 2 }}{2}\).

Tương tự tâm, bán kính đường tròn ngoại tiếp tam giác OAD lần lượt là trung điểm F của AD và \(\frac{{R\sqrt 2 }}{2}\). Gọi H là trung điểm của DC và giao điểm của tia OH và cung nhỏ CD là K. Dễ thấy K là điểm chính giữa của cung nhỏ DC và KD = KO = KC = R. Vậy tâm và bán kính đường tròn ngoại tiếp tam giác ODC lần lượt là K và R.

b) Do \(\widehat {CAB} = \widehat {DBA} = {45^o}\) nên \(\widehat {AIB} = {90^o}\) hay AC vuông góc với BD. Mặt khác AB = R, BC = AD = \(R\sqrt 2 \) và DC = \(R\sqrt 3 \)do đó bán kính đường tròn ngoại tiếp của các tam giác IAB, IBC, IAD, IDC lần lượt là: \(\frac{R}{2};\frac{{R\sqrt 2 }}{2};\frac{{R\sqrt 2 }}{2};\frac{{R\sqrt 3 }}{2}\).