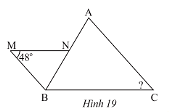
Giải bài 7 trang 71 SGK Toán 8 tập 2– Chân trời sáng tạoTrong Hình 19, cho biết Đề bài Trong Hình 19, cho biết \(MN//BC,MB//AC\) a) Chứng minh rằng \(\Delta BNM\backsim\Delta ABC\) b) Tính \(\widehat C\)
Video hướng dẫn giải Phương pháp giải - Xem chi tiết - Nếu hai góc của tam giác này bằng hai góc của tam giác kia thì hai tam giác đố đồng dạng với nhau. - Hai tam giác đồng dạng thì các góc tương ứng bằng nhau. Lời giải chi tiết a) Vì \(MN//BC\) nên \(\widehat {MNB} = \widehat {CBA}\) (hai góc so le trong) Vì \(MB//AC\) nên \(\widehat {MBN} = \widehat {CAB}\) (hai góc so le trong) Xét tam giác \(BNM\) tam giác \(ABC\) ta có: \(\widehat {MNB} = \widehat {CBA}\) (chứng minh trên) \(\widehat {MBN} = \widehat {CAB}\) (chứng minh trên) Do đó, \(\Delta BNM\backsim\Delta ABC\) (g.g) b) Vì \(\Delta BNM\backsim\Delta ABC\) nên \(\widehat M = \widehat C = 48^\circ \) (hai góc tương ứng).  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
