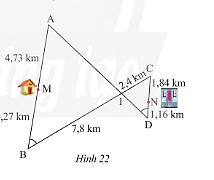
Giải bài 10 trang 72 SGK Toán 8 tập 2– Chân trời sáng tạoĐường đi và khoảng cách từ nhà anh Thanh Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên Đề bài Đường đi và khoảng cách từ nhà anh Thanh (điểm \(M\)) đến công ty (điểm \(N\)) được thể hiện trong Hình 22. Hãy tìm con đường ngắn nhất để đi từ nhà anh Thanh đến công ty. Video hướng dẫn giải Phương pháp giải - Xem chi tiết - Nếu hai góc của tam giác này bằng hai góc của tam giác kia thì hai tam giác đố đồng dạng với nhau. - Hai tam giác đồng dạng thì các cặp cạnh tương ứng có cùng tỉ lệ. Lời giải chi tiết Ta có: \(AB = AM + MB = 4,73 + 4,27 = 9m\);\(CD = CN + ND = 1,84 + 1,16 = 3m\) Xét tam giác \(AIB\) tam giác \(CID\) ta có: \(\widehat {ABI} = \widehat {CDI}\) (giả thuyết) \(\widehat {AIB} = \widehat {CID}\) (hai góc đối đỉnh) Do đó, \(\Delta AIB\backsim\Delta CID\) (g.g) Suy ra, \(\frac{{AB}}{{CD}} = \frac{{AI}}{{CI}} = \frac{{BI}}{{DI}} \Leftrightarrow \frac{9}{3} = \frac{{AI}}{{2,4}} = \frac{{7,8}}{{DI}}\). Ta có: \(\frac{9}{3} = \frac{{AI}}{{2,4}} \Rightarrow AI = \frac{{9.2,4}}{3} = 7,2m\);\(\frac{9}{3} = \frac{{7,8}}{{ID}} \Rightarrow ID = \frac{{3.7,8}}{9} = 2,6m\). Các con đường đi từ nhà anh Thanh đến công ty là: Con đường: \(MB \to BI \to IC \to CN\) có độ dài là: \(MB + BI + IC + CN = 4,27 + 7,8 + 2,4 + 1,84 = 16,31km\) Con đường: \(MB \to BI \to ID \to DN\) có độ dài là: \(MB + BI + ID + DN = 4,27 + 7,8 + 2,6 + 1,16 = 15,83km\) Con đường: \(MA \to AI \to ID \to DN\) có độ dài là: \(MA + AI + ID + DN = 4,73 + 7,2 + 2,6 + 1,16 = 15,69km\) Con đường: \(MA \to AI \to IC \to CN\) có độ dài là: \(MA + AI + IC + CN = 4,73 + 7,2 + 2,4 + 1,84 = 16,17km\) Vậy đi theo con đường \(MA \to AI \to ID \to DN\) là ngắn nhất.
|