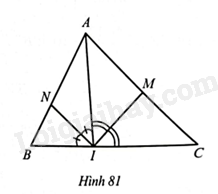
Giải bài 68 trang 85 sách bài tập toán 8 – Cánh diều

Đề bài

Cho tam giác $ABC$ có ba góc nhọn, điểm $I$ thuộc cạnh $BC$ và $IM,IN$ lần lượt là đường phân giác của các góc $AIC$ và $AIB$. Chứng minh: $AN.BI.CM=BN.IC.AM$.

Lời giải chi tiết

Áp dụng tính chất đường phân giác vào các tam giác $ABI,AIC$ ta có: $\frac{AN}{NB}=\frac{AI}{BI};\frac{CM}{MA}=\frac{IC}{AI}$.

Suy ra $\frac{BI}{IC}.\frac{AN}{NB}.\frac{CM}{MA}=\frac{BI}{IC}.\frac{AI}{BI}.\frac{IC}{AI}=1$

Do đó $AN.BI.CM=BN.IC.AM$.