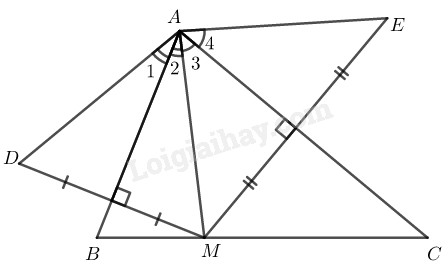
Bài 60 trang 86 SBT toán 8 tập 1Giải bài 60 trang 86 sách bài tập toán 8. Cho tam giác ABC có A = 70 độ, điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC... Đề bài Cho tam giác \(ABC\) có \(\widehat A = {70^0}\), điểm \(M\) thuộc cạnh \(BC.\) Vẽ điểm \(D\) đối xứng với \(M\) qua \(AB,\) vẽ điểm \(E\) đối xứng với \(M\) qua \(AC.\) \(a)\) Chứng minh rằng \(AD = AE.\) \(b)\) Tính số đo góc \(DAE.\) Phương pháp giải - Xem chi tiết +) Sử dụng định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của đoạn thẳng nối hai điểm đó. +) Sử dụng tính chất đường trung trực: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó. +) Trong tam giác cân, đường trung tuyến ứng với cạnh đáy cũng là đường trung trực, đường phân giác. Lời giải chi tiết
\(a)\) Vì \(D\) đối xứng với \(M\) qua trục \(AB\) \(⇒ AB\) là đường trung trực của \(MD.\) \(⇒ AD = AM\) (tính chất đường trung trực) \((1)\) Vì \(E\) đối xứng với \(M\) qua trục \(AC\) \(⇒ AC\) là đường trung trực của \(ME\) \(⇒ AM = AE\) ( tính chất đường trung trực) \((2)\) Từ \((1)\) và \((2)\) suy ra : \(AD = AE\) \(b)\) \(AD = AM\) suy ra \(∆ AMD\) cân tại \(A\) có \(AB ⊥ MD\) nên \(AB\) cũng là đường phân giác của góc \(MAD\) \( \Rightarrow {\widehat A_1} = {\widehat A_2}\) \(AM = AE\) suy ra \(∆ AME\) cân tại \(A\) có \(AC ⊥ ME\) nên \(AC\) cũng là đường phân giác của \(\widehat {MAE}\) \( \Rightarrow {\widehat A_3} = {\widehat A_4}\) \(\widehat {DAE} = {\widehat A_1} + {\widehat A_2} + {\widehat A_3} + {\widehat A_4}\) \(= 2\left( {{{\widehat A}_2} + {{\widehat A}_3}} \right) \)\(= 2\widehat {BAC}\)\( = {2.70^0} = {140^0}\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
