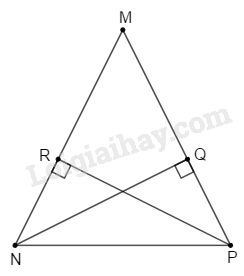
Bài 60 trang 100 Vở bài tập toán 7 tập 2Giải bài 60 trang 100 VBT toán 7 tập 2. Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân... Đề bài Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều. Phương pháp giải - Xem chi tiết Ta chứng mình tam giác cân bằng cách chứng minh hai cạnh bên bằng nhau. Lời giải chi tiết
Giả sử tam giác MNP có hai góc nhọn là ˆN và ˆP; hai đường cao NQ và PR bằng nhau. Ta sẽ chứng minh tam giác MNP cân tại M. Vì góc N nhọn nên chân đường cao xuất phát từ đỉnh P là điểm R thuộc MN (R ở giữa M và N). Tương tự, Q ở giữa M và P. Hai tam giác vuông MNQ và MPR có góc M chung, NQ=PR (giả thiết) nên ΔMNQ=ΔMPR, suy ra MN=MP, hay tam giác MNP cân tại M. Theo chứng minh trên, tam giác có ba đường cao bằng nhau thì nó sẽ lần lượt cân tại cả ba đỉnh của tam giác đó. Do đó, tam giác có ba đường cao bằng nhau là một tam giác đều. HocTot.Nam.Name.Vn
|